第 $1$ 章 複 素 数
$\S\ 6.$ 一般の一次有理函数 $\boldsymbol{w=\dfrac{\ \alpha z+\beta\ }{\ \gamma z+\delta\ }.}$
$\boldsymbol{1.}$ 一次の有理函数の一般な形は\[w=\frac{\alpha z+\beta}{\hphantom{1}\gamma z+\delta\hphantom{1}}\]で,係数 $\alpha$,$\beta$,$\gamma$,$\delta$ は任意の複素数である.ただし $\alpha\delta-\beta\gamma\neq0$ と仮定する.$\large*$ $^{\large*}\ $以下,本節で,いちいちことわらないで,この条件を仮定する. さもなければ $w$ は定数(または無意味)になる.$\gamma=0$ ならば,$w$ は一次の整函数になる.その場合を除いて,$\gamma\neq0$ とすれば\[w=\frac{\hphantom{1}\alpha\hphantom{1}}{\gamma}-\frac{\alpha\delta-\beta\gamma}{\gamma^2\left(z+\dfrac{\delta}{\gamma}\right)\ }\]すなわち\begin{alignat*}{3}&w=\lambda+\mu w^\prime,&\hphantom{m}&\lambda=\frac{\hphantom{1}\alpha\hphantom{1}}{\gamma},&\hphantom{m}&\mu=-\frac{\ \alpha\delta-\beta\gamma\ }{\gamma^2},\\[2mm]&w^\prime=\frac{1}{\hphantom{1}z^\prime\hphantom{1}},&&&&\\[2mm]&z^\prime=z-\nu,&&\nu=-\frac{\hphantom{1}\delta\hphantom{1}}{\gamma},&&\\[2mm]\end{alignat*}とおくことができる.このように $w$ と $z$ の間へ $w^\prime$,$z^\prime$ という二つの変数を入れて見れば,$z^\prime$ は $z$ の一次整函数,$w^\prime$ は $z^\prime$ の逆数,$w$ は $w^\prime$ の一次整函数で,いずれもすでに説明した場合になる.$z$ が円を描けば,$z^\prime$ も円を描き,したがって $w^\prime$ も,また $w$ も円を描くから,一般の一次有理函数による写像においても,円には円が対応するのである.また相対応する角が同じ向きに相等しいことも明白である.
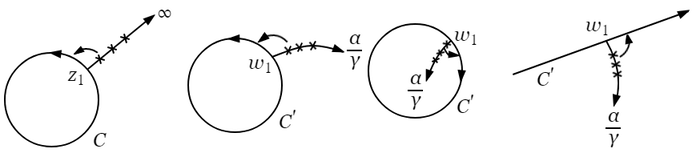
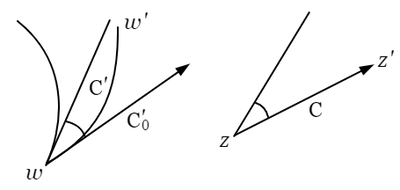
$z$ が円周 $\mathrm{C}$ を描くとき,$w$ が円周 $\mathrm{C}^\prime$ を描くとする.このいい表わし方は粗雑であるが,$z$ が円周 $\mathrm{C}$ の上を一周するときに,それに対応して $w$ は $\mathrm{C}^\prime$ の周上を一周する.一周というのは,円周上の一点から出発して回転の向きを変えずに出発点まで帰る意味である.このことは一次整函数および逆数の場合の証明を回想すれば容易にわかる.
さて,この一周には二つの向きがある.仮に時計の針と反対の向きを正の向きとすれば $z$ が正の向きに $\mathrm{C}$ を一周するとき,$w$ は $\mathrm{C}^\prime$ を正の向きに一周するか,または負の向きに一周するか,これら二つの場合の区別が重要である.この区別は,$z$ 平面上 $\mathrm{C}$ の内部が $w$ 平面上 $\mathrm{C}^\prime$ の内部に対応するか,外部に対応するかに関係する.$\mathrm{C}$ の周上の一点 $z_1$ から半径の延長線を引いて見る.$z$ が $z_1$ からこの直線上を $\infty$ まで進行するとすれば,それに対応して $w$ は $\mathrm{C}^\prime$ の周上で $z_1$ に対応する点 $w_1$ からある円弧の上を $z=\infty$ に対応する $w=\alpha/\gamma$ まで進行するであろう.しかもその間に再び円周 $\mathrm{C}^\prime$ を横切ることはない.その上に相対応する角が同じ向きに相等しいということがある.
そこで $\alpha/\gamma$ が円 $\mathrm{C}^\prime$ の外部にあるときには,$w$ は $\mathrm{C}^\prime$ の上を正の向きに一周するが,$\alpha/\gamma$ が円 $\mathrm{C}^\prime$ の内部にあるならば,$w$ は $\mathrm{C}^\prime$ の上を負の向きに一周する(次の図を参照).
$z$ から $\infty$ に至る直線の中途にある任意の $z$(すなわち円 $\mathrm{C}$ の外部にある任意の $z$)に対応する $w$ に関しても同様で,その $w$ が $\mathrm{C}^\prime$ の外部にあるか,または内部にあるかに従って,$w$ が $\mathrm{C}^\prime$ の周上を一周する向きが正または負になるのである.
$\mathrm{C}$ または $\mathrm{C}^\prime$ が直線である場合も同様で,円の内部または外部というところが直線の一側または他側に代わるだけである.
 |
すなわち円板が円の内部ならば,時計の針と反対の向きが正で,円板が円の外部ならば,その反対が正の向きになる.また直線を円の特別の場合と見て,その直線の一側を円板とよぶならば,直線のその側を左手に見ながら進行する向きを正の向きとするのである.
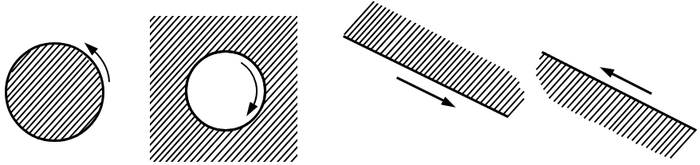 |
〔定理 $\boldsymbol{1.\ 3}$〕 一次有理函数による写像においては$\hspace{0.5mm}$,$\hspace{-0.5mm}$円板は円板に対応し$\hspace{0.5mm}$,$\hspace{-0.5mm}$その限界線上の正の向きは正の向きに対応する.
$\boldsymbol{2.}$ 一般の一次式において,分母分子を $z$ の係数でくくれば\[w=\kappa\frac{z-\omega}{\hphantom{1}z-\omega^\prime\hphantom{1}}\]の形になる.$\kappa=1$ のときは,特に簡明である.
〔問題 $\boldsymbol{1}$〕 $w=\dfrac{z-\omega}{\hphantom{1}z-\omega^\prime\hphantom{1}}$ による写像において,$w$ 平面上 $0$ を中心とする円と,$0$ を通る直線とに対応する $z$ 平面上の円を求めること.
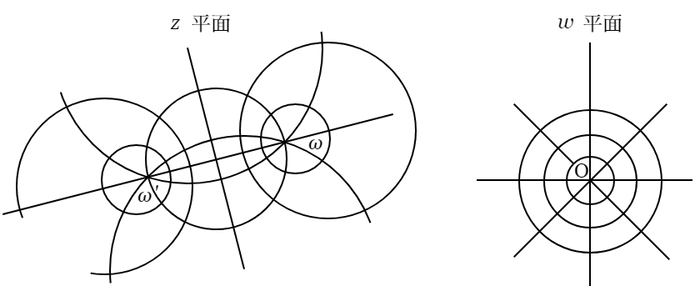 |
ゆえにそれに対応する $z$ 平面上の円周の上では,\[\frac{|z-\omega|}{\ |z-\omega^\prime|\ }=c.\] これは $\omega$,$\omega^\prime$ に関する Apollonius の円である.また $\operatorname{arc}\ \!w=\theta$ なる直線に対応する円周上では $\angle\omega^\prime zw=\theta$.この円は $\omega$,$\omega^\prime$ を通って Apollonius の円と直交する.
〔注意〕 一般の場合において,$z$ の二つの値 $z_1$,$z_2$ に,$w$ の二つの値 $w_1$,$w_2$ が対応するとき,$z$ 平面で,$z_1$,$z_2$ を通る円の束と,それに直交する円の束とを考察する.後者は $z_1$,$z_2$ に関する Apollonius の円である.$w$ 平面で,これらに対応するものは,$w_1$,$w_2$ を通る円の束と,$w_1$,$w_2$ に関する Apollonius の円の束である.問題 $1$ は $w_1$,$w_2$ が $0$,$\infty$ なる特別の場合にすぎない.
問題 $1$ の写像を球面上で考察すれば,興味ある幾何学上の結果が得られる.
$w$ 平面における $0$ を通る直線は,球面上では $0$ と $\infty$ とを通る大円周に対応し,$0$ を中心とする平面上の円は,球面上ではこれらの大円周に直交する円周になる.すなわちこれらの二組の円は $\infty$ と $0$ とを両極とする経緯度線である.
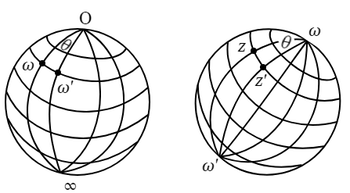 |
いま $\omega\omega^\prime$ を軸として $z$ 球面を回転させるとき,任意の点 $z$ が $z^\prime$ の位置に来たとして,それらに対応する $w$ 球面上の点を $w$,$w^\prime$ とすれば,回転の角を $\theta$ とするとき,\[w^\prime=\kappa w,\hspace{15mm}\kappa=\cos\theta+i\sin\theta\]であることは明白である.よって $z$ と $z^\prime$ の間には\[\frac{\hphantom{1}z^\prime-\omega\hphantom{1}}{\hphantom{1}z^\prime-\omega^\prime\ }=\kappa\frac{\hphantom{1}z-\omega\hphantom{1}}{\hphantom{1}z-\omega^\prime\hphantom{1}}\tag{$\ 1\ $}\]なる関係が成り立つ.ただし $\omega$ と $\omega^\prime$ とは対極点であるから,$\overline{\omega}\omega^\prime=-1$($\S\ 5$,問題 $3$).
あるいは,また $\left(\ 1\ \right)$ において\[\omega=\frac{\hphantom{1}l+mi\hphantom{1}}{1+n},\hspace{5mm}\omega^\prime=-\frac{\hphantom{1}l+mi\hphantom{1}}{1-n},\hspace{5mm}\varepsilon=\cos\frac{\theta}{2}+i\sin\frac{\theta}{2}\]とおけば,\[\overline{\varepsilon}\frac{z^\prime(1+n)-(l+mi)}{z^\prime(1-n)+(l+mi)}=\varepsilon\frac{z(1+n)-(l+mi)}{z(1-n)+(l+mi)}.\]これを $z^\prime$ に関して解けば\[z^\prime=\frac{(d+ci)z+(b-ai)}{\ -(b+ai)z+(d-ci)\ }\tag{$\ 2\ $}\]を得る.ただし $a=l\sin\dfrac{\theta}{2}$,$b=m\sin\dfrac{\theta}{2}$,$c=n\sin\dfrac{\theta}{2}$,$d=\cos\dfrac{\theta}{2}$,$a^2+b^2+c^2+d^2=1$.
$\left(\ 2\ \right)$ は Cayley の公式である.
$\left(\ 2\ \right)$ を出すには $1-n^2=(l+mi)(l-mi)$ に注意することを要する.
このように,回転は複素数を用いて $\left(\ 1\ \right)$ または $\left(\ 2\ \right)$ によって簡明に表わされる.これを実数で表わせば,次の問題が解かれるであろう.
「空間における直交軸の原点を通る方向余弦 $l$,$m$,$n$ なる直線を軸として角 $\theta$ だけの回転によって,点 $X$,$Y$,$Z$ が $X^\prime$,$Y^\prime$,$Z^\prime$ の位置に来るとするとき,$X^\prime$,$Y^\prime$,$Z^\prime$ を $X$,$Y$,$Z$ で表わすこと」.
これはつまり直交軸の変換であるから,$X^\prime$,$Y^\prime$,$Z^\prime$ は $X$,$Y$,$Z$ の一次式として出て来なければならない.計算の結果は次のとおり.\[\left.\begin{alignat*}{1}&X^\prime=(a^2+d^2-b^2-c^2)X+2(ab-cd)Y+2(ac+bd)Z,\\[2mm]&Y^\prime=2(ab+cd)X+(b^2+d^2-a^2-c^2)Y+2(bc-ad)Z,\\[2mm]&Z^\prime=2(ac-bd)X+2(ad+bc)Y+(c^2+d^2-a^2-b^2)Z.\end{alignat*}\right\}\] 実際計算するには,$(X,\ Y,\ Z)=(1,\ 0,\ 0)$,$(0,\ 1,\ 0)$,$(0,\ 0,\ 1)$ すなわち $z=1$,$i$,$0$ に対応する $z^\prime$ を $\left(\ 2\ \right)$ から求めて,それらの $z^\prime$ に対応する $(X^\prime,\ Y^\prime,\ Z^\prime)$ を$\S\ 5$,問題 $3$ の公式から求めるがよい.
$\boldsymbol{3.}$ 一次の有理函数\[w=\frac{\hphantom{1}\alpha z+\beta\hphantom{1}}{\gamma z+\delta}\]は係数 $\alpha$,$\beta$,$\gamma$,$\delta$ の比が与えられたときにまったく確定する.ゆえに概括的にいえば,三つの条件を与えて,それらを満たす一次有理函数を求めることができる.特に円は三つの点によって定まるから,$z$ 平面と $w$ 平面とにおいて与えられた円を互いに対応させるような一次有理函数が求められるであろう.
〔問題 $\boldsymbol{2}$〕 一次有理函数\[w=\frac{\hphantom{1}\alpha z+\beta\hphantom{1}}{\gamma z+\delta}\]において,$z$ と $w$ との相対応する四組の値を\[z,\hphantom{1}w;\hphantom{1}z_1,\hphantom{1}w_1;\hphantom{1}z_2,\hphantom{1}w_2;\hphantom{1}z_3,\hphantom{1}w_3\]とすれば\[\frac{\hphantom{1}w-w_2\hphantom{1}}{w-w_3}:\frac{\hphantom{1}w_1-w_2\hphantom{1}}{w_1-w_3}=\frac{\hphantom{1}z-z_2\hphantom{1}}{z-z_3}:\frac{\hphantom{1}z_1-z_2\hphantom{1}}{z_1-z_3}\] これは簡単な計算の問題である.\begin{alignat*}{1}w_1-w_2&=\frac{\ \alpha z_1+\beta\ }{\gamma z_1+\delta}-\frac{\hphantom{1}\alpha z_2+\beta\hphantom{1}}{\gamma z_2+\delta}\\[2mm]&=\frac{\hphantom{1}(\alpha\delta-\beta\gamma)(z_1-z_2)\hphantom{1}}{(\gamma z_1+\delta)(\gamma z_2+\delta)}\end{alignat*}などからすぐに出て来る.
〔注意〕 上の等式の両辺に出ている比を四つの数 $(w,\ w_1;\ w_2,\ w_3)$ または $(z,\ z_1;\ z_2,\ z_3)$ の非調和比という.よって上の定理は次のようにいい表わされる.
「非調和比は一次変形によって不変である」.
〔問題 $\boldsymbol{3}$〕 相対応する三組の値\[z_1,\hphantom{1}w_1;\hphantom{1}z_2,\hphantom{1}w_2;\hphantom{1}z_3,\hphantom{1}w_3\]が与えられたとき,$z$ の一次有理函数 $w$ を求めること.
| 〔解〕 | \[\frac{\hphantom{1}w-w_2\hphantom{1}}{w-w_3}:\frac{\hphantom{1}w_1-w_2\hphantom{1}}{w_1-w_3}=\frac{\hphantom{1}z-z_2\hphantom{1}}{z-z_3}:\frac{\hphantom{1}z_1-z_2\hphantom{1}}{z_1-z_3}\] |
〔注意〕 一次有理函数によって,$z$ 平面の円に $w$ 平面の円が対応することは,上の定理からも導かれる.すなわち $z$ が $z_1$,$z_2$,$z_3$ を通る円を描くとき,右辺の非調和比は実数値をもつ.したがって左辺において $w$ は $w_1$,$w_2$,$w_3$ を通る円周を描くのである($\S\ 3$,問題 $6$).
〔問題 $\boldsymbol{4}$〕 $w=\dfrac{\hphantom{1}\alpha z+\beta\hphantom{1}}{\gamma z+\delta}$ によって,$z$ 平面の円 $\mathrm{C}$ に,$w$ 平面の円 $\mathrm{C}^\prime$ が対応するならば,$\mathrm{C}$ に関して互いに反転な二つの点には,$\mathrm{C}^\prime$ に関して互いに反転な二つの点が対応する.
〔解〕 $z_1$,$z_2$ を $\mathrm{C}$ に関して互いに反転とし,それらに対応する $w$ 平面の二点を $w_1$,$w_2$ とする.$z_1$,$z_2$ を通る円 $\mathrm{K}$ は $\mathrm{C}$ に直交するから,それに対応する $w_1$,$w_2$ を通る円 $\mathrm{K}^\prime$ は $\mathrm{C}^\prime$ に直交する.このように互いに対応する円を二組作ったとすれば,$w_1$,$w$ は $\mathrm{C}^\prime$ に直交する二つの円の交点である.したがって $\mathrm{C}^\prime$ に関して互いに反転である.
$\mathrm{C}^\prime$ が直線である場合には,$w_1$,$w_2$ は $\mathrm{C}^\prime$ に関して互いに対称である.
これによって,円に関する反転を,直線に関する対称の拡張とみなして,円に関する反転を対称ともよぶ.また円に関して互いに反転なる点を互いに鏡像ともいう.特に単位円に関する $z$ の鏡像を $z^{\Large*}$ とすれば,$z^{\Large*}=1/\overline{z}$,すなわち $z^{\Large*}$ は $z$ の共役の逆数である.
〔問題 $\boldsymbol{5}$〕 単位円をそれ自身に対応させる一次有理函数は\[w=\frac{\hphantom{1}\alpha z-\beta\hphantom{1}}{\overline{\beta}z-\overline{\alpha}}\tag{$\ 1\ $}\]$\alpha$,$\beta$ は任意であるが,ただ $|\alpha|\neq|\beta|$ であることを要する.
〔解〕 $w=0$,$\infty$ は単位円に関して互いに対称であるから,それらに対応する $z$ の値も単位円に関して互いに対称でなければならない.ゆえに $w=0$ に $z=\mu$ が対応するとすれば($|\mu|\neq1$),$w=\infty$ には $\mu$ の反転である $\dfrac{1}{\ \!\overline{\mu}\ \!\ \!}$ が対応する.したがって $w$ の形は\[w=\kappa\hspace{0.7mm}\cdotp\frac{\hphantom{1}z-\mu\hphantom{1}}{\overline{\mu}z-1}.\tag{$\ 2\ $}\]しかるに,$z=0$,$\infty$ に対応する $w$ の値すなわち $\kappa\mu$ と $\dfrac{\kappa}{\ \!\overline{\mu}\ \!\ \!}$ とも互いに反転でなければならないから\[\overline{\kappa}\overline{\mu}\hspace{0.7mm}\cdotp\frac{\kappa}{\ \!\overline{\mu}\ \!\ \!}=1.\]
| したがって | \[|\kappa|=1.\] |
$w=0$ に $z=\infty$ が対応する場合は $\left(\ 2\ \right)$ には洩れているが,この場合には $w=\dfrac{\ \kappa\ }{z}$,$|\kappa|=1$ で,すなわち $\left(\ 1\ \right)$ において $\alpha=0$ である場合である.
逆に $\left(\ 1\ \right)$ が実際単位円を単位円に対応させることは,$|z|=1$ であるとき\[w\overline{w}=\frac{\ az-\beta\ }{\overline{\beta}z-\overline{\alpha}}\hspace{0.7mm}\cdotp\frac{\ \overline{\alpha}\overline{z}-\overline{\beta}\ }{\beta\overline{z}-\alpha}=\frac{\ \alpha z-\beta\ }{\overline{\beta}z-\overline{\alpha}}\hspace{0.7mm}\cdotp\frac{\ \overline{\alpha}-z\overline{\beta}\ }{\beta-\alpha z}=1\]からわかる.
$z$ 平面の単位円の内部が $w$ 平面の単位円の内部に対応するか,または外部に対応するかは,$z=0$ に対応する $w$ の絶対値が $1$ よりも小であるか,または大であるかによる.すなわち $|\beta|\lessgtr|\alpha|$,$\left(\ 2\ \right)$ ならば,$|\mu|\lessgtr1$ による.
〔問題 $\boldsymbol{6}$〕 $z$ 平面の実数軸を $w$ 平面の単位円に対応させる一次有理函数の一般の形は\[w=\kappa\frac{\hphantom{1}z-\mu\hphantom{1}}{z-\overline{\mu}},\hspace{1cm}|\kappa|=1.\] 〔解〕 $w=0$,$\infty$ に対応する $z$ の値は実数軸に関して互いに対称すなわち共役複素数でなければならないから,$w$ の形は上のとおりである.また $z=\infty$ に対応する $w=\kappa$ は単位円の上にあることを要するから $|\kappa|=1$.
ゆえに,$\kappa=\dfrac{\ \alpha\ }{\overline{\alpha}}$ とおくことができる.そこで $\alpha\mu=-\beta$ とおけば,\[w=\frac{\hphantom{1}\alpha z+\beta\hphantom{1}}{\overline{\alpha}z+\overline{\beta}}\]ここで $z$ を実数とすれば,分母分子は互いに共役,したがって $|w|=1$.
$\boldsymbol{4.}$ 一般に $z$ は $z^\prime$ の一次有理函数,$z^\prime$ は $z^{\prime\prime}$ の一次有理函数であるとすれば,$z$ は $z^{\prime\prime}$ の一次有理函数である.いま\begin{alignat*}{1}z\hphantom{^\prime}&=\frac{\hphantom{1}\alpha z^\prime+\beta\hphantom{1}}{\gamma z^\prime+\delta},\tag{$\ 1\ $}\\[2mm]z^\prime&=\frac{\hphantom{1}\alpha^\prime z^{\prime\prime}+\beta^{\ \prime}\hphantom{1}}{\gamma^\prime z^{\prime\prime}+\delta^\prime}\tag{$\ 2\ $}\end{alignat*}とすれば,第一式の $z^\prime$ に第二式から代入して\[z=\frac{\hphantom{1}(\alpha\alpha^\prime+\beta\gamma^\prime)z^{\prime\prime}+(\alpha\beta^{\ \prime}+\beta\delta^\prime)\hphantom{1}}{\hphantom{1}(\gamma\alpha^\prime+\delta\gamma^\prime)z^{\prime\prime}+(\gamma\beta^{\ \prime}+\delta\delta^\prime)\hphantom{1}}\tag{$\ 3\ $}\]を得る.$z^\prime$ 平面から $z$ 平面への写像 $\left(\ 1\ \right)$ を $S$ という文字で表わし,$z^{\prime\prime}$ 平面から $z^\prime$ 平面への写像 $\left(\ 2\ \right)$ を $S^\prime$ という文字で表わすとき,$\left(\ 3\ \right)$ は $z^{\prime\prime}$ 平面から $z$ 平面への写像を表わす.これを $S$,$S^\prime$ という二つの写像から合成されたものといい,それを表わすのに $SS^\prime$ という記号を用いる.これは群論の記法である.この記法では文字の順序に注意しなければならない.$SS^\prime$ と $S^\prime S$ とは意味が違う.
$\left(\ 1\ \right)$,$\left(\ 2\ \right)$,$\left(\ 3\ \right)$ における函数的関係を上と同じ文字で表わすならば\[z=S\left(z^\prime\right),\hphantom{z}z^\prime=S^\prime\left(S^{\prime\prime}\right)\hspace{5mm}したがって\hspace{5mm}z=S\left\{S^\prime\left(z^{\prime\prime}\right)\right\}\]で,この最後の記号の括弧を略して\[z=SS^\prime\left(z^{\prime\prime}\right)\]とすれば,上の群論上の記法と一致する.
$\left(\ 1\ \right)$,$\left(\ 2\ \right)$ のような関係式で重要なのは,その係数であって,$z$,$z^\prime$,$z^{\prime\prime}$ などの文字はただ変数が三つあることを示すだけである.よって係数のみを標記して\[S=\begin{pmatrix}\alpha&\beta\\\gamma&\delta\end{pmatrix},\hspace{1cm}S^\prime=\begin{pmatrix}\alpha^\prime&\beta^{\ \prime}\\\gamma^\prime&\delta^\prime\end{pmatrix}\]とする.しからば\[SS^\prime=\begin{pmatrix}\alpha\alpha^\prime+\beta\gamma^\prime&\alpha\beta^{\ \prime}+\beta\delta^\prime\\\gamma\alpha^\prime+\delta\gamma^\prime&\gamma\beta^{\ \prime}+\delta\delta^\prime\end{pmatrix}\underset{\overset{}{.}}{}\tag{$3^{\Large*}$}\] また $\left(\ 1\ \right)$ を $z^\prime$ に関して解けば,$z^\prime$ が $z$ の一次有理函数として表わされる.すなわち\[z^\prime=\frac{\delta z-\beta}{-\gamma z+\alpha}.\]これは上の $z^\prime$ から $z$ への写像 $S$ の逆である.これを $S^{-1}$ としるすならば,\[S^{-1}=\begin{pmatrix}\hphantom{-}\delta&-\beta\\-\gamma&\hphantom{-}\alpha\end{pmatrix}.\tag{$\ 4\ $}\] 上のことを念頭において再び問題 $6$ を考察して見るならば,その解決が明らかになるであろう.
いま $z^\prime=S\left(z\right)$ を $z$ 平面と $z^\prime$ 平面との実数軸を互いに対応させる任意の一次有理函数とし,また $w=T\left(z^\prime\right)$ は $z^\prime$ 平面の実数軸を $w$ 平面の単位円に対応させるある一つの特定の一次有理函数とする.しからば $w=TS\left(z\right)$ は $z$ 平面の実数軸を $w$ 平面の単位円に対応させるであろう.実際 $z$ が実数ならば $S\left(z\right)$ は実数,したがって $T\left\{S\left(z\right)\right\}$ は単位円周上になければならないのである.
逆に $w=S^\prime\left(z\right)$ を $z$ 平面の実数軸を $w$ 平面の単位円に対応させる任意の一次有理函数とすれば,$z^\prime=T^{-1}S^\prime(z)$ によって $z$ 平面と $z^\prime$ 平面との実数軸が互いに対応するであろう.実際 $z$ が実数値を取るとき,$S^\prime(z)$ は単位円周上にあるから,$T^{-1}\{S^\prime(z)\}$ は実数軸上にあるのである.よって\[T^{-1}\{S^\prime(z)\}=S(z)\]とおいてさしつかえない.したがって\[S^\prime(z)=T\{S(z)\}.\]ゆえに $S^\prime$ を求めることは $TS$ を求めることに帰する.
さて,問題 $7$ によって実数軸を実数軸に対応させる $S$ の一般の形は,明らかに\[S=\begin{pmatrix}a&b\\c&d\end{pmatrix},\hspace{1cm}a,\hphantom{1}b,\hphantom{1}c,\hphantom{1}d\hphantom{1}は実数.\]また\[w=\frac{\hphantom{1}z^\prime+i\hphantom{1}}{z^\prime-i}\]とすれば,明らかに $z^\prime$ の実数値に $|w|=1$ なる値が対応するから,\[T=\begin{pmatrix}1&\hphantom{-}i\\1&-i\end{pmatrix}\]とすることができる.ゆえに $\left(3^{\Large*}\right)$ によって\[TS=\begin{pmatrix}a+ci&b+di\\a-ci&b-di\end{pmatrix}=\begin{pmatrix}\alpha&\beta\\\overline{\alpha}&\overline{\beta}\end{pmatrix}.\]$\alpha=a+ci$,$\beta=b+di$ とおいたのである.これは問題 $6$ で求めた一般の一次有理函数の形である.
なお,ついでながら問題 $5$ を考察する.
$S$,$T$ の意味は上のとおりとすれば,$z$ が単位円周上にあるとき,$T^{-1}(z)$ は実数,したがって $ST^{-1}(z)$ も実数,したがって $TST^{-1}(z)$ は単位円周上にある.ゆえに $TST^{-1}$ なる結合によって問題 $5$ の解が得られる.この結合を実行するに,$TS$ は上のとおりであるから,それに $\left(\ 4\ \right)$ から得られる\[T^{-1}=\begin{pmatrix}i&\hphantom{1}i\\1&-1\end{pmatrix}\]を結合して\[\begin{array}{l}TST^{-1}=\begin{pmatrix}\alpha&\beta\\\overline{\alpha}&\overline{\beta}\end{pmatrix}\begin{pmatrix}i&\hphantom{-}i\\1&-1\end{pmatrix}=\begin{pmatrix}\alpha i+\beta&\alpha i-\beta\\\overline{\alpha}i+\overline{\beta}&\overline{\alpha}i-\overline{\beta}\end{pmatrix}\\[2mm]\begin{alignat*}{2}\alpha i+\beta&=\lambda&\hspace{5mm}&とすれば\hspace{5mm}\overline{\alpha}i-\overline{\beta}=-\lambda,\\[2mm]\alpha i-\beta&=-\mu&\hspace{5mm}&とすれば\hspace{5mm}\overline{\alpha}i+\overline{\beta}=\overline{\mu}.\end{alignat*}\end{array}\]よって\[TST^{-1}=\begin{pmatrix}\lambda&-\mu\\\overline{\mu}&-\overline{\lambda}\end{pmatrix}.\]これは問題 $5$ の公式と記号が違うだけである.
$\boldsymbol{5.}$ 一次函数による写像において,円に円が対応することと,相対応する角の相等しいこととが,本節の問題の骨髄であるが,一次函数のこれら二つの性質が,あまりに混み入って説明されたのであった.円に円が対応することは一次函数の特性であるけれども,相対応する角が相等しいことは一次函数特有の性質ではないのである.\[w=\frac{\hphantom{1}\alpha z+\beta\hphantom{1}}{\gamma z+\delta}\]において,$z^\prime$ に $w^\prime$ が対応するとすれば\[w^\prime=\frac{\hphantom{1}\alpha z^\prime+\beta\hphantom{1}}{\gamma z^\prime+\delta}.\]したがって\[w-w^\prime=(z-z^\prime)\frac{\alpha\delta-\beta\gamma}{\hphantom{1}(\gamma z+\delta)(\gamma z^\prime+\delta)\hphantom{1}}\]\[\frac{\hphantom{1}w-w^\prime\hphantom{1}}{z-z^\prime}=\frac{\alpha\delta-\beta\gamma}{\hphantom{1}(\gamma z+\delta)(\gamma z^\prime+\delta)\hphantom{1}}.\]いま $z^\prime$ が限りなく $z$ に近づくものとすれば,極限において\[\underset{z^\prime\rightarrow z}{\operatorname{Lim}}\frac{\hphantom{1}w-w^\prime\hphantom{1}}{z-z^\prime}=\frac{\alpha\delta-\beta\gamma}{\hphantom{1}(\gamma z+\delta)^2\hphantom{1}}.\]この右辺を $\kappa$ とおけば\[\underset{z^\prime\rightarrow z}{\operatorname{Lim}}\frac{\hphantom{1}w-w^\prime\hphantom{1}}{z-z^\prime}=\kappa\]で,$z^\prime$ がどのような向きから $z$ に近づくとしても,$\kappa$ は一定である.
すなわち $\operatorname{arc}\ \!(w-w^\prime)$ と $\operatorname{arc}\ \!(z-z^\prime)$ との差は,極限において,一定の値 $\operatorname{arc}\ \!\kappa$ をもつのである.
 |
このように考えると,相対応する角の相等しいことは\[\underset{z^\prime\rightarrow z}{\operatorname{Lim}}\frac{\hphantom{1}w-w^\prime\hphantom{1}}{z-z^\prime}\]が一定の値をもつことからの帰結である.この極限は実数の場合における微分商に該当するものであるから,それを $\dfrac{\hphantom{1}dw\hphantom{1}}{dz}$ としるすが,実数の場合には,$z^\prime$ が $z$ に近づく向きは左右両方に限るのに反して,変数が複素数であるときは,$z^\prime$ は各方面から $z$ に近づき得るにもかかわらず,一定の極限が存在するのである.
このように一定の微分商が存在する場合には,上の証明がそのまま当てはまるから,相対応する角は同じ向きに相等しいのである.ただし微分商 $\kappa$ が $0$ に等しいときは例外である.その場合には $\operatorname{arc}\ \!\kappa$ は不定であるから,上の証明を適用することができない.
付 記
この所で現代の数学における複素数の位置に関して解説を試みようと思う.負数の平方根が実数中に存在しないことから生ずる不便を除くために,複素数を導入して数の範囲を拡張したのであるが,複素数の範囲内では,四則に関する計算の原則が実数の場合そのままの形で保存されると同時に,負数の開平のみでなく,任意の複素数の開法が例外なく可能である.それのみではない,開法は方程式 $z^n-\alpha=0$ の解であるが,一般に複素数を係数とする任意の方程式 $f(x)=0$ の解が複素数の範囲内で可能である.この定理は代数学の基本定理といわれるもので,次の章においてその証明を述べるであろうが,これによって見れば,方程式の解法を主要の問題とする代数学においては,複素数の全範囲を考察の対象とすべきことは当然である.
Gauss は $1799$ 年にその学士論文で代数学の基本定理の証明を発表した後,整数論の問題に複素数を適用して偉大な成功をもたらし,次いで Cauchy は函数論を複素変数の上に築いて,$18$ 世紀の微積分法にまつわった多くの疑問に光明を与え,Abel および Jacobi の楕円函数の発見を可能にする素地を作った.また射影幾何学の発達は,幾何学においても,虚数的原素を導入することの避くべからざることを示した.いずれの方面においても,実数は数学の対象としては不自然に偏狭で,複素数の範囲においてのみ,数学の諧調的,統一的の発達が可能であることが認められて,今日の数学は複素数の数学となったのである.
このようにして,$19$ 世紀の中頃に至って,虚数が一般数学界において承認された後に $1$,$i$ を原素とする二次元の複素数の範囲を更に拡張して多次元の複素数を数学に導入することが問題となった.Hamilton の四元法(quaternions)や,Grassmann の広延論(Ausdehnungslehre)がその最初の試みで,今日では,このような高次元の複素数を高級複素数という.しかるに,ここに最も注意すべき事実は,これらの高級複素数においては,四則に関する原則を全部保存することが不可能であるということである.四則に関する原則は $\S\ 1$,$\left(\ 1\ \right)\sim\left(\ 9\ \right)$ に掲げた加法および乗法に関する交換,結合,分配の法則と減法および除法の一意性とである.除法の一意性から,積が $0$ であるとき,因数のあるものが必ず $0$ である,という法則 $\left(10\right)$ が生ずる.いま,なるべくこれらの原則を敬重して,数の範囲を拡張しようとすると,加法,減法のみに関しては問題は簡単であるが,乗法,除法に関しては結合,分配の法則を犯さないとすれば,交換の法則と除法の一意性とのうち,どちらかを犠牲にすることを避けることができない.交換の法則が成り立たないとすれば,数学は随分面倒になるが,除法の一意性が失われるならば,混雑は更にはなはだしい.$0$ でないものを掛け合わせて $0$ が出るようでは迷惑至極である.
この事実は数学における複素数(われわれの複素数,$x+yi$)の位置を明示する.実数だけでは数の範囲は狭きに失するが,だからといって高級複素数までを入れては数学はむずかしくなる.近頃,代数という語を複数にして algebras という.それは種々の高級複素数の代数があり得ることが,あたかも異なる公理の上に種々の幾何学が成り立ち得るのと同様であるからである.そうすれば,種々の幾何学の中での Euclid の幾何学と同様に,種々の代数学の中で $x+yi$ の代数学が一番手頃で,したがって一番役立つということになる.
上のように四則の原則を全部保存するとすれば,数の範囲は通常の複素数の外に出ることができないということは,比較的簡単に証明することができるから,参考として迅速にその大要を述べることにする.
実数単位 $1$ のほかに新単位 $\mathbf{i}$,$\mathbf{j}$,$\cdots$,$\mathbf{k}$ を用いて,実数 $a$,$b$,$c$,$\cdots$,$d$ を係数として,\[z=a+b\mathbf{i}+c\mathbf{j}+\cdots+d\mathbf{k},\]のような式を一つの数という.このような数の四則が上の原則を全部保存して定められたと仮定する.そうすれば,\begin{alignat*}{5}z&=\hphantom{^\prime}\!a&&+\hphantom{^\prime}\!b\mathbf{i}&&+\hphantom{^\prime}\!c\mathbf{j}&&+\cdots&&+\hphantom{^\prime}\!d\mathbf{k},\\[2mm]z^2&=a^\prime&&+b^\prime\mathbf{i}&&+c^\prime\mathbf{j}&&+\cdots&&+d^\prime\mathbf{k},\\[2mm]z^3&=a^{\prime\prime}&&+b^{\prime\prime}\mathbf{i}&&+c^{\prime\prime}\mathbf{j}&&+\cdots&&+d^{\prime\prime}\mathbf{k},\\[2mm]\cdots&\hphantom{=^{\prime\prime}}\cdots&&\hphantom{+^{\prime\prime}}\cdots&&\hphantom{+^{\prime\prime}}\cdots&&\hphantom{+^{\prime\prime}}\!\cdots&&\hphantom{+^{\prime\prime}}\cdots\end{alignat*}のような等式が生ずるから,実数 $c_1$,$c_2$,$\cdots$,$c_n$ を適当に定めるならば,\[z^n+c_1z^{n-1}+\cdots+c_n=0\tag{$\ 1\ $}\]のような関係が生ずる(連立一次方程式の解法,参照).
さて,代数学の基本定理によれば\[x^n+c_1x^{n-1}+\cdots+c_n\]のような実係数をもつ多項式は,一次の実因数 $x-a$ または二次の実因数 $x^2+mx+n$ の積に分解される.ただしこの二次因数に関しては $x^2+mx+n=0$ は実根をもたないものとするのである.さて,いわゆる新しい数 $z$ は実数と同様の四則の法則に従うという仮定であるから,実数に関して\[x^n+c_1x^{n-1}+\cdots+c_n=(x-a)\cdots(x^2+mx+n)\cdots\]のような恒等式が成り立つならば,必ず\[z^n+c_1z^{n-1}+\cdots+c_n=(z-a)\cdots(z^2+mz+n)\cdots\]なる関係が成り立たねばならない.しかるに $\left(\ 1\ \right)$ によって,この等式の左辺は $0$ に等しく,そして積が $0$ に等しいときには,因数の中に $0$ に等しいものがあるという仮定であるから\[z=a\hspace{5mm}または\hspace{5mm}z^2+mz+n=0\]すなわち $z$ は実数でないならば,虚根もつ二次方程式を満足しなければならない.
さて\[x^2+mx+n=(x-h)^2+k^2\tag{$h$,$k\ $は実数$\ k\neq0$}\]のような恒等式が成り立つから,上述のように\[z^2+mz+n=(z-h)^2+k^2=0,\]ゆえに\[z=h+k\mathbf{J}\]とおけば,\[\mathbf{J}^2=-1.\]ゆえに $\mathbf{J}$ は $i$ または $-i$ に等しく,したがって $z$ は $h+ki$ または $h-ki$ に等しい.等しいというのは記号の違いを度外においていうのである.すなわち四則の計算に関しては $\mathbf{J}$ も $i$ または $-i$ もまったく同様の動作をするのをいうのである.$z$ は新しい数であるといっても,それは $h\pm ki$ が記号だけを変えて新しい数と名乗って出て来たのにすぎない.さて $\left(\ 2\ \right)$ のような数は $\pm\mathbf{J}$ のほかにはない.実際 $\mathbf{J}^{\prime2}=-1$ とすれば,$\mathbf{J}^{\prime2}-\mathbf{J}^2=0$,すなわち $(\mathbf{J}^\prime-\mathbf{J})(\mathbf{J}^\prime+\mathbf{J})=0$.ゆえに $\mathbf{J}^\prime-\mathbf{J}=0$ または $\mathbf{J}^\prime+\mathbf{J}=0$,すなわち $\mathbf{J}^\prime=\pm\mathbf{J}$.よって $z^\prime$ を新範囲における任意の数とするとき,$z^\prime$ が実数でないならば,$h^\prime+k^\prime\mathbf{J}$ のような形であって,新範囲といっても,それは内容において,われわれの複素数とまったく同一である.