第 $2$ 章 方程式論の基本定理
$\S\ 9.$ 代数学の基本定理
$\boldsymbol{1.}$ 次に述べる代数学の基本定理の証明は三段に分かれる.まず,その第一段を独立の一定理として初めに片付ける.〔定理 $\boldsymbol{2.\ 3}$〕 一次以上の多項式 $f(z)$ が $z$ に $\alpha$ という値を与えたときに $0$ にならないとする.$f(\alpha)\neq0$.しからば,どんなに $\alpha$ に近いところでも,$z$ を適当に取って,$|f(z)|\lt|f(\alpha)|$ とすることができる.
また $f(\alpha)$ は $0$ であっても,$0$ でなくても,$|f(z)|\gt|f(\alpha)|$ とすることもできる.
〔注意〕 前段は $f(\alpha)\neq0$ という仮定がなくては意味をなさない.後段は基本定理の証明には必要でないが,問題それ自身の興味のために,一緒に証明するのである.
〔証〕 $f(z)$ を $n$ 次の多項式として,$\alpha$ の近くに取ろうとする $z$ を $\alpha+h$ とおく.$z=\alpha+h$.
$f(z)$ すなわち $f(\alpha+h)$ を $h$ の昇冪に排列すれば\[f(\alpha+h)=f(\alpha)+Bh+Ch^2+\cdots+Lh^n,\hphantom{11}(L\neq0)\]のような形になるが,$B$,$C$,$\cdots$ などが $0$ になる場合もあり得るから,それも引きくるめて考察するために,\[f(\alpha+h)=f(\alpha)+ah^e+bh^{e+1}+\cdots+lh^n\]というようにしるして $a\neq0$ とする.$a$,$b$,$\cdots$,$l$ などの式を計算する必要はない.ただそれらは $h$ には関係のない定数であることだけに注意すればよろしい.上の式を更に次のように書く.\[f(\alpha+h)=f(\alpha)+ah^e(1+\varTheta).\tag{$\ 1\ $}\]すなわち,ここで\[\varTheta=\frac{b}{a}h+\cdots+\frac{l}{a}h^{n-e}.\tag{$\ 2\ $}\]
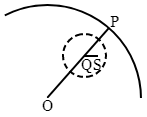 |
上の $(\ 2\ )$ の $\varTheta$ の式を見れば,$|\varTheta|\lt1$ にするには,$|h|$ を適当に小さくすればよい.前に $|h|$ に課された条件 $(\ 4\ )$ は $|h|$ がある限界以内にあることであったから,つまり $|h|$ を適当に小さくとれば $(\ 4\ )$ と $(\ 5\ )$ とを同時に満足させることができる.すなわち定理の前段が証明されたのである.
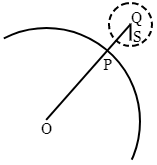
後段の証明も同様である.ただ $ah^e$ を表わすベクトルを $\mathrm{OP}$ の延長の上にとって,$\mathrm{QS}\lt\mathrm{PQ}$ にすればよい.
 |
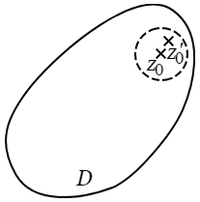 |
したがって $|f(z)|$ の最も大きくなる点は必ず区域の限界線上になければならない.また $f(z)$ がこの区域内において $0$ にならない限り区域内の一点 $z_0$ において $|f(z)|$ が最小の値をもつこともない.したがって $|f(z)|$ の最小である点は区域の限界線上になければならない.対偶をいえば,区域の限界線上で $|f(z)|$ が最小にならないならば,$f(z)$ は必ず区域の内部のある点で $0$ にならなければならない.これが基本定理の証明の根拠になるのである.
ある区域にその限界線をも属させていわゆる閉じた区域を考えるときは,その区域に属するある点において連続函数は最大(または最小)の値を実際に取るという定理は承認されたものとみなす.限界線を区域に属させないとき,すなわち,いわゆる開区域では,そうはいわれない.最大または最小がちょうど限界線上の点において起こることがあるからである.
$\boldsymbol{3.}$ 以上を前おきにすれば,基本定理の証明は容易である.
〔定理 $\boldsymbol{2.\ 4}$〕 代数方程式は必ず根をもつ.
このような場合に,方程式というのはもちろん一次以上の方程式をいうのである.
〔証〕 方程式を $f(z)=0$ として,$z$ に任意の値 $\alpha$ を与える.そのとき $f(z)=0$ ならば,$\alpha$ がすなわち根である.よって $f(\alpha)\neq0$ とする.定理 $2.\ 2$ によって $|z|$ を十分に大きくすれば,$|f(z)|$ をいくらでも大きくすることができるから,$z$ を表わす複素数平面上において,$0$ を中心として $\alpha$ を含む適当な円を描いて,その円周上の各点において $|f(z)|\gt|f(\alpha)|$ とすることができる(定理 $2.\ 2$).そうすれば,$z$ をこの円内で変動させるときに,$|f(z)|$ の最も小さくなるのは,円周上の点ではない(そのために上の円内に $\alpha$ を含ませておいたのである).したがってこの円内において,$f(z)$ が $0$ になるところがなければならない.すなわち基本定理が証明されたのである.
代数学の基本定理は Gauss が初めて証明した.Gauss の証明は三つあるが上の証明は Cauchy の方法によったもので,普通,代数書に掲載されるものである.Gauss の第三証明は,その形を変えて,函数論の書に掲載される.本書で後に再び他の証明を掲げるであろう.
$\boldsymbol{4.}$ 基本定理が証明された上は,$n$ 次の多項式が $n$ 個の一次因数に分解されることが確定する($\S\ 7$).
もし一次因数の中に相等しいものがあれば,それらを一つの冪にまとめて(記号を変えて)しるせば,\begin{alignat*}{1}&f(z)=a_0(z-\alpha)^a(z-\beta)^b\cdots(z-\lambda)^l,\\[2mm]&\alpha\neq\beta\neq\cdots\neq\lambda,\hspace{1cm}a+b+\cdots+l=n.\end{alignat*}$a_0$ は $f(z)$ における $n$ 次の項の係数である($a_0\neq0$).
〔問題 $\boldsymbol{1}$〕 上の分解はただ一様に限る.
〔解〕 $\alpha^\prime$ を $\alpha$,$\beta$,$\cdots$,$\lambda$ と異なる数とするとき,$f(z)$ が $z-\alpha^\prime$ のような因数をもち得ないことは明らかである.もしそのような因数があるとすれば,$f(\alpha^\prime)=0$ すなわち $a_0(\alpha^\prime-\alpha)^a(\alpha^\prime-\beta)^b\cdots(\alpha^\prime-\lambda)^l=0$.$a_0\neq0$,$\alpha^\prime-\alpha\neq0$,$\cdots$,$\alpha^\prime-\lambda\neq0$ だから,これは不可能である($\S\ 1$.$(10)$).
ゆえに上と違った分解が可能ならば,一次因数は同じでも,指数が違うことになろう.たとえば $f(z)$ は一次因数 $z-\alpha$ の $a$ よりも大きい指数をもつ冪 $(z-\alpha)^m$,$m=a+e$,$e\gt0$ で割り切れて\[a_0(z-\alpha)^a(z-\beta)^b\cdots=(z-\alpha)^{a+e}\mathrm{P}(z)\]のような等式が,$z$ のすべての値に対して成り立つことになる.$\mathrm{P}(z)$ は多項式である.このような等式が不可能であることは,多項式の連続性によっても証明される.$z=a$ 以外の任意の値を与えるならば,$z-\alpha\neq0$ だから,両辺を $(z-\alpha)^a$ で割って\[a_0(z-\beta)^b\cdots=(z-\alpha)^e\mathrm{P}(z)\]を得る.$z\rightarrow\alpha$ のとき,左辺$\rightarrow a_0(\alpha-\beta)^b\cdots\neq0$,右辺$\rightarrow0$.これは矛盾である(参照,$\S\ 22$,$3$).
$f(z)$ が一次因数 $z-\alpha$ をちょうど $k$ 回だけ含むとき,$\alpha$ を $f(z)$ の $k$ 次の根という.$k\gt1$ のとき総称して複根という.$k$ がその重複度数である.$\S\ 7$,$2$ 公式 $(\ 2\ )$ から見えるように,$\alpha$ が $k$ 次の根であることの鑑別条件は\[f(\alpha)=0,\hphantom{1}f^\prime(\alpha)=0,\hphantom{1}\cdots,\hphantom{1}f^{(k-1)}(\alpha)=0,\hphantom{1}f^{(k)}(\alpha)\neq0\]である(参照,$\S\ 22$,$3$).
〔問題 $\boldsymbol{2}$〕 実係数をもつ多項式が虚根 $\alpha$ をもつときには,それと共役な虚根 $\overline{\alpha}$ をももつ.しかもそれらの重複度数は相等しい.
〔解〕 $f(z)$ の係数が実数であるから,$f(\alpha)$ と $f(\overline{\alpha})$ とは互いに共役である.ゆえに $f(\alpha)=0$ ならば,$f(\overline{\alpha})=0$.複根の場合には $f^\prime(x)$,$f^{\prime\prime}(x)$,$\cdots$ をも考察すればよい.$f^\prime(\alpha)=f^{\prime\prime}(\alpha)=\cdots=f^{(k-1)}(\alpha)=0$,$f^{(k)}(\alpha)\neq0$ ならば,$f^\prime(\overline{\alpha})=f^{\prime\prime}(\overline{\alpha})=\cdots=f^{(k-1)}(\overline{\alpha})=0$,$f^{(k)}(\overline{\alpha})\neq0$.