第 $2$ 章 方程式論の基本定理
$\S\ 10.$ 根 の 連 続 性
$\boldsymbol{1.}$ 任意の多項式 $f(z)$ と複素数平面上の単純な閉曲線(二重点をもたない閉曲線)$C$ とが与えられたとして,$z$ が $C$ の上を正の向きに($C$ の内部を左に見ながら)一周して元の位置に帰るとすると,それに伴って $f(z)$ は連続的に変動するが,その際 $\operatorname{arc}\ \!f(z)$ は結局どれだけの増減をするであろうか.〔定理 $\boldsymbol{2.\ 5}$〕 $f(z)=0$ の根のうち $k$ 個($k\geqq0$,複根は重複度数を数える)が単純な閉曲線 $C$ の内部にあって,その他は $C$ の外部にあるならば,$z$ が $C$ の上を正の向きに一周するとき,$\operatorname{arc}\ \!f(z)$ は $2k\pi$ だけ増加する.
〔証〕 いま $f(z)$ を $n$ 次とし,$C$ の内部にある根を $\alpha_1$,$\alpha_2$,$\cdots$,$\alpha_k$,$C$ の外部にある根を $\beta_1$,$\beta_2$,$\cdots$,$\beta_{n-k}$ とする.すなわち\[f(z)=a(z-\alpha_1)(z-\alpha_2)\cdots(z-\alpha_k)(z-\beta_1)(z-\beta_2)\cdots\]とする.しからば\[\operatorname{arc}\ \!f(z)=\operatorname{arc}\ \!a+\underset{\alpha}{\textstyle\sum}\operatorname{arc}\ \!(z-\alpha)+\underset{\beta}{\textstyle\sum}\operatorname{arc}\ \!(z-\beta)\]
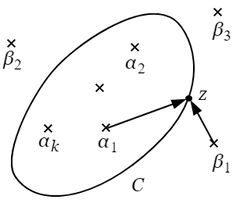 |
さて $z$ が $C$ を正の向きに一周するとき $\operatorname{arc}\ \!(z-\alpha)$ は各々 $2\pi$ だけ増加し,また $\operatorname{arc}\ \!(z-\beta)$ には結局増減がないことは右の図から見て明白である.ゆえに $\operatorname{arc}\ \!f(z)$ は $2k\pi$ だけ増加する.
 |
また上の考察は偏角 $\operatorname{arc}\ \!f(z)$ が連続的に変動することを緊要の条件とするので,この条件なしには意味をなさない.よって曲線 $C$ が $f(z)=0$ の根を通過する場合を除外したのである.$\alpha$ が $C$ の上の点ならば, $^{\large*}\ \alpha$ が $C$ の周上で,多角形の頂点のような「かど」になってはいないと仮定していう.$\operatorname{arc}\ \!(z-\alpha)$ は,$z$ が $\alpha$ を通過するに際して突然 $\pi$ だけの変動をする.あるいはすでに変動が連続的でないとする以上,$\pi$ の任意の奇数倍に等しい変動をするといってもさしつかえないであろう$\large*$.
$\boldsymbol{2.}$ 上の定理 $2.\ 5$ を証明するのに,代数学の基本定理,すなわち $n$ 次の多項式 $f(z)$ が $n$ 個の一次因数に分解されることを根拠とした.この基本定理を使わないで,証明を試みるならば,次のようになる.
$C$ の内部にある $f(z)=0$ の根を $\alpha_1$,$\alpha_2$,$\cdots$,$\alpha_k$ とすれば,各根に一次因数が伴うから($\S\ 7$,$4$),\[f(z)=(z-\alpha_1)\cdots(z-\alpha_k)\varphi(z)\]を得る.$\varphi(z)$ は $C$ の内部には根をもたない多項式である.ゆえに\[\operatorname{arc}\ \!f(z)={\textstyle\sum}\operatorname{arc}\ \!(z-\alpha)+\operatorname{arc}\ \!\varphi(z)\]であるから,$z$ が $C$ を一周するとき,$\operatorname{arc}\ \!\varphi(z)$ の増加が $0$ であることがわかればよい.それを $\varphi(z)$ を一次因数に分解しないで,ただ $\varphi(z)$ の連続性のみを根拠として証明しようというのである.
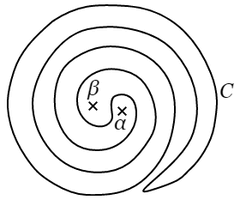
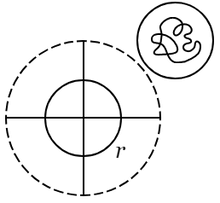
$z$ が $C$ の上またはその内部($C$ を境界とするこの閉じた面分を $D$ と名づける)にあるとき,$\phi(z)$ は $0$ にならないという仮定だから,$D$ における $|\varphi(z)|$ の最小値を $M$ とすれば,$M\gt0$.いま $r$ を $M$ よりも小さいある定まった数,たとえばきまりをつけるために $r=\dfrac{M}{2}$ とする.$w=\varphi\left(z\right)$ を表わす複素数平面上,原点を中心,$r$ を半径とする円を $\varGamma$ とすれば,$z$ が $D$ において運動するときに,$w$ は $\varGamma$ の外部にあって,かつ $\varGamma$ までの距離が $r$ よりも近くなることはない.
 |
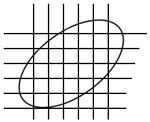
この手順を繰り返して,面分 $D$ を幾つの部分に分けても同様であるから,いま $z$ 平面上に方眼を引いて $D$ を $N$ 個の部分に分けたとする(図 $2$).
 |
 |
$\boldsymbol{3.}$ 定理 $2.\ 5$ から次の定理が得られる.
〔定理 $\boldsymbol{2.\ 6}$〕 (Rouché の定理) 単一な閉曲線 $C$ の上で,多項式 $\psi(z)$ が絶対値において $\varphi\left(z\right)$ よりも小ならば,$\varphi\left(z\right)$ と $\varphi\left(z\right)+\psi(z)$ とは $C$ の内部において同数の根をもつ.
〔証〕 $C$ の上で $|\psi(z)|\lt|\varphi\left(z\right)|$.ゆえに $\varphi\left(z\right)$ は $C$ の上で $0$ にならない.(このことは定理の言明の中に入れておくのが親切であったかも知れない)また $C$ の上で $\varphi\left(z\right)+\psi(z)$ も $0$ にならない.ゆえに $C$ の内部にある根の数が同数であることを示すには,$z$ が $C$ を一周するときの $\operatorname{arc}\ \!\varphi\left(z\right)$ と $\operatorname{arc}\ \!\{\varphi\left(z\right)+\psi(z)\}$ との増加が相等しいことを見ればよい.さて\[\varphi\left(z\right)+\psi(z)=\varphi\left(z\right)\left(1+\frac{\ \psi(z)}{\varphi\left(z\right)}\right),\]\[\operatorname{arc}\ \!\{\varphi\left(z\right)+\psi(z)\}=\operatorname{arc}\ \!\varphi\left(z\right)+\operatorname{arc}\ \!\left(1+\frac{\ \psi(z)}{\varphi\left(z\right)}\right)\]で,$z$ が $C$ を一周するとき,仮定によって $\left|\dfrac{\ \psi(z)\ }{\varphi\left(z\right)}\right|\lt1$ であるから,\[1+\dfrac{\ \psi(z)\ }{\varphi\left(z\right)}\]は $1$ を中心として $1$ よりも小さい半径をもつ円の内部に止まる.したがってその $\operatorname{arc}$ の増加は $0$ である.すなわち定理にいってある通り.
$\boldsymbol{4.}$ 上の定理を応用すれば,代数学の基本定理の簡単な証明ができる.\[f(z)=a_0z^n+a_1z^{n-1}+\cdots+a_n\]とすれば,$|z|=R$ を適当に大きく取るとき,\[|a_0z^n|\gt|a_1z^{n-1}+\cdots+a_n|\]になることは前に述べた.よって Rouché の定理で,$C$ を $|z|=R$ なる円,$\varphi=a_0z^n$,$\psi=a_1z^{n-1}+\cdots+a_n$ とすれば,$f(z)$ は $C$ の内部に $n$ 個の根をもつことが知られるのである.
$\boldsymbol{5.}$ Rouché の定理を応用して,なお一つの定理を証明する.
〔定理 $\boldsymbol{2.\ 7}$〕 代数方程式の根は係数の連続函数である.
〔証〕 まず定理の意味を説明する.方程式\[f(z)\equiv a_0z^n+a_1z^{n-1}+\cdots+a_n=0\]において,係数 $a_0$,$a_1$,$\cdots$,$a_n$ が変動するならば,根も変動するであろうが,各係数の変動の範囲を適当に小さく制限することによって,根の変動を予定の範囲内に止まらせることができるというのである.
証明すべきことは,複根の場合をも考慮していえば,次のようになる.根の変動は,絶対値において,$\delta$ 以内と限定する.
$z_0$ を $f(z)=0$ の $k$ 重根とする($k\geqq1$).
$z_0$ を中心,$r$($\leqq\delta$)を半径とする円を $C$ とする.ただし $C$ は内部にも周の上にも,$z_0$ の外の根を含まないと仮定する.$r\leqq\delta$ であるから,それはさしつかえない.
そこで,係数 $a_0$,$a_1$,$\cdots$,$a_n$ を $a_0+h_0$,$a_1+h_1$,$\cdots$,$a_n+h_n$ に変えるのであるが,適当に $\varepsilon$ を定めて,$|h_0|\lt\varepsilon$,$|h_1|\lt\varepsilon$,$\cdots$,$|h_n|\lt\varepsilon$ とすれば,係数変更後の方程式\[f(z)+\psi(z)\equiv f(z)+h_0z^n+h_1z^{n-1}+\cdots+h_n=0\]は円 $C$ の内部にちょうど $k$ 個の根をもつであろう.
このことが証明されるならば,係数変動後の方程式の各根は原方程式のある根からの距離において,予定の制限 $\delta$ を越えることがないのである.
問題がこのように整理された上は,その解決は容易である.
仮定によって,$C$ の周上で $f(z)$ は $0$ にならないから,$C$ の周上での $|f(z)|$ の最小値を $m$ とすれば,$m\gt0$.
$C$ の周上での $|z|$ の最大値を $M$ とし,$|h_0|$,$|h_1|$,$\cdots$,$|h_n|$ の最大の値を $h$ とすれば,$C$ の周上で\[|\psi(z)|=|h_0z^n+h_1z^{n-1}+\cdots+h_n|\leqq h(M^n+M^{n-1}+\cdots+M+1).\]よって $\varepsilon$ を十分小さく取って,$h\lt\varepsilon$ とすれば,$C$ の周上で\[|\psi(z)|\lt m すなわち |\psi(z)|\lt|f(z)|.\]そこで Rouché の定理によって\[f(z)+\psi(z)=0\]は $C$ の内部において $f(z)=0$ と同数の根,すなわち $k$ 個の根をもつのである.
〔問題 $\boldsymbol{1}$〕 $n$ 次の方程式 $f(z)=0$ が単位円内($|z|\lt1$)に $m$ 個,円外に $m^\prime=n-m$ の根をもつとする(周上にはない).しからば,\begin{alignat*}{1}f(z)&=a_0z^n+a_1z^{n-1}+\cdots+a_n,\\[2mm]f^{\Large*}(z)&=\overline{a}_nz^n+\overline{a}_{n-1}z^{n-1}+\cdots+\overline{a}_0\end{alignat*}とするとき,方程式\[f(z)+\lambda f^{\Large*}(z)=0\tag{$\ 1\ $}\]は,$(1^\circ)$ $|\lambda|\lt1$ ならば,単位円内に $m$ 個,円外に $m^\prime$ 個の根をもつ.$(2^\circ)$ $|\lambda|\gt1$ ならば,単位円内に $m^\prime$ 個,円外に $m$ 個の根をもつ.$(3^\circ)$ $|\lambda|=1$ ならば,単位円の周上に少なくとも $|m-m^\prime|$ 個(単位円の内外に同数)の根をもつ.
〔解〕 $f(z)=a_0(z-\alpha_1)(z-\alpha_2)\cdots(z-\alpha_n)$ とすれば,\[f^{\Large*}(z)=\overline{a}_0(1-\overline{\alpha}_1z)(1-\overline{\alpha}_2z)\cdots(1-\overline{\alpha}_nz)\]で,$f^{\Large*}(z)$ の根は単位円周に関して $f(z)$ の根の鏡像である($\S\ 6$,$3$).ゆえに\[\frac{f(z)}{\ f^{\Large*}(z)\ }=\frac{a_0}{\ \overline{a}_0\ }{\textstyle\prod}\frac{z-\alpha_k}{\ 1-\overline{\alpha}_kz\ },\]したがって単位円周上において($|z|=1$),$\left|\dfrac{f(z)}{f^{\Large*}(z)}\right|=1$ ($\S\ 6$,問題 $5$).
仮定によって $f(z)$ は単位円周上には根をもたない.しからば $|\lambda|\lt1$ のとき,単位円周上において\[\left|\frac{\ \lambda f^{\Large*}(z)\ }{f(z)}\right|\lt1.\] ゆえに Rouché の定理によって単位円内における $(\ 1\ )$ の根の数は $m$ である.$|\lambda|\gt1$ の場合は $f$ と $f^{\Large*}$ とを交換して考えればよい.
$|\lambda|=1$ の場合は根の連続性による.いま練習のためにその方法を説明する.$(\ 1\ )$ において $\lambda$ に $|\lambda|=1$ なる一定の値を与えたとするとき,$(\ 1\ )$ の根は単位円の内部,外部に $N$ ずつ,周上に $N_0$ あるとする.$\large*$ $^{\large*}\ |\lambda|=1$ だから,$\lambda=\mu/\overline{\mu}$ として,$(\ 1\ )$ を $F(z)=\overline{\mu}f(z)+\mu f^{\Large*}(z)=0$ と書くことができる.しからば $F(z)=F^{\Large*}(z)$.したがって $\alpha$ が $(\ 1\ )$ の根ならば,$1/\overline{\alpha}$ も $(\ 1\ )$ の根だから,$(\ 1\ )$ は単位円の内外に同数の根をもつ.\[N_0+2N=n.\] 内部または外部にある根から単位円周までの最短距離を $r$ とする.根の連続性によって $\lambda$ を十分小さい範囲内において変動させるとき,各根の変位を $r$ 以内の距離に限ることが出来るから,この範囲内において $\lambda$ の近くに,$|\lambda_1|\lt1$ である $\lambda_1$ または $|\lambda_2|\gt1$ である $\lambda_2$ を取って見る.しからば $(\ 1\ )$ において $\lambda$ に $\lambda_1$ を代入するとき,その根のうち $N$ は確かに単位円の内部に,また他の $N$ は確かに単位円の外部にある.しかるに,上の証明によって $\lambda=\lambda_1$ のとき $(\ 1\ )$ は単位円の内部に $m$ 個,外部に $m^\prime$ 個の根をもつのであるから,\[m\geqq N,\hspace{15mm}m^\prime\geqq N,\]ゆえに\[2m+N_0\geqq n,\hspace{13mm}2m^\prime+N_0\geqq n\]\[N_0\geqq n-2m=m^\prime-m\hspace{12mm}N_0\geqq n-2m^\prime=m-m^\prime.\]すなわち\[N_0\geqq|m-m^\prime|.\] 〔注意〕 $f(z)$ が単位円周上に根 $\alpha$ をもてば,$\dfrac{\ 1\ }{\overline{\alpha}}=\alpha$ であるから,$\alpha$ は $f^{\Large*}(z)$ の根である.この場合には,$f(z)$ からそれらの根を省いておいて,上の定理を適用することができる.