第 $2$ 章 方程式論の基本定理
$\S\ 12.$ Hermite の定理および拡張
$\boldsymbol{1.}$ 〔定理 $\boldsymbol{2.\ 9}$〕 方程式 $f(z)=0$ の根の虚数部の符号が全部同一であるとき,係数の実部と虚部とを分けて $f(z)=U(z)+iV(z)$ とすれば,$U(z)=0$ も $V(z)=0$ も実根のみをもって,かつ $U(z)$ の根と $V(z)$ の根とは互いに隔離する(Hermite または Biehler の定理).〔注意〕 $f(z)=a_0z^n+a_1z^{n-1}+\cdots+a_n$,$a_0=b_0+c_0i$,$a_1=b_1+c_1i$,$\cdots$
とすれば\begin{alignat*}{1}U(z)&=b_0z^n+b_1z^{n-1}+\cdots+b_n,\\[2mm]V(z)&=c_0z^n+c_1z^{n-1}+\cdots+c_n.\end{alignat*} $U(z)$ と $V(z)$ とのうち一方だけは $n$ 次よりも低いこともある($b_0=0$ または $c_0=0$ のとき).
また $U(z)$ と $V(z)$ との根が互いに隔離するというのは,根がいずれも単根で,大小の順序において $U(z)$ の相接する二つの根の間に $V(z)$ の一つの根があり,また $V(z)$ の相接する二つの根の間に $U(z)$ の根が一つあるのをいう.
〔証〕 便宜上 $f(z)=0$ の根は実数軸の上側にあるとする.$U(z)=0$ または $V(z)=0$ の根がみな実数であることを,Hermite は次のように証明した.
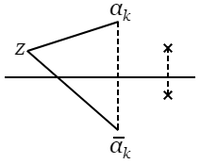
$f(z)$ の各係数を共役なる複素数でおき換えるときに生ずる多項式を $\overline{f}(z)$ とする.しからば\[U=\frac{f+\overline{f}}{2},\hspace{7mm}V=\frac{f-\overline{f}}{2i}\]である.また $f(z)=a_0(z-\alpha_1)(z-\alpha_2)\cdots(z-\alpha_n)$ とすれば,\[\overline{f}(z)=\overline{a}_0(z-\overline{\alpha}_1)(z-\overline{\alpha}_2)\cdots(z-\overline{\alpha}_n)\]で,仮定によって $\overline{\alpha}_1$,$\overline{\alpha}_2$,$\cdots$,$\overline{\alpha}_n$ は実数軸の下側にある.
さて,方程式 $U(z)=0$ は\[f(z)+\overline{f}(z)=0,\]または\[\frac{\ f(z)\ }{\overline{f}(z)}=-1\]と書くことができる.すなわち\[\frac{\ a_0\ }{\overline{a}_0}\ \frac{\ z-\alpha_1\ }{\ z-\overline{\alpha}_1\ }\ \hspace{0.7mm}\cdotp\ \frac{\ z-\alpha_2\ }{\ z-\overline{\alpha}_2\ }\ \cdots\ \frac{\ z-\alpha_n\ }{\ z-\overline{\alpha}_n\ }=-1.\tag{$\ 1\ $}\] いま $z$ を実数軸の上側または下側に取れば,\[\left|\dfrac{\ z-\alpha_k\ }{\ z-\overline{\alpha}_k\ }\right|\lt1 または \gt1.\]
 |
$V(z)=0$ についても同様である.この場合には,$(\ 1\ )$ の右辺を $+1$ にして考えればよい.
この証明では,$U(z)=0$ と $V(z)=0$ との根が実数であることははなはだ明瞭に示されるけれども,その根の位置の関係については,何等の知識をも与えない.それは後回しにして,上の証明によって直ちに定理そのものの拡張が得られる.すなわち
$f(z)=0$ の根が実数軸の上側にあるときは,方程式\[\frac{\ f(z)\ }{\overline{f}(z)}=\lambda\tag{$\ 2\ $}\]の根は\begin{alignat*}{1}|\lambda|=1 &ならば みな 実数,\\[2mm]|\lambda|\gt1 &ならば みな 実数軸の下側,\\[2mm]|\lambda|\lt1 &ならば みな 実数軸の上側\end{alignat*}にある.前と同様に $(\ 2\ )$ の両辺の絶対値を比較すれば,直ぐにわかるのである.$U$,$V$ で $(\ 2\ )$ を表わせば\[U+iV=\lambda(U-iV),\]すなわち\[(1-\lambda)U+i(1+\lambda)V=0,\]すなわち\[U+\frac{\ i(1+\lambda)}{1-\lambda}V=0.\]よって\[\frac{\ i(1+\lambda)\ }{1-\lambda}=\kappa\tag{$\ 3\ $}\]とおけば\[U+\kappa V=0.\]さて $(\ 3\ )$ によって(参照,$\S\ 6$,$34$ 頁)\begin{alignat*}{1}|\lambda|=1 &ならば, \kappa\ は実数,\\[2mm]|\lambda|\gt1 &ならば, \kappa\ は実数軸の下側にあり,\\[2mm]|\lambda|\lt1 &ならば, \kappa\ は実数軸の上側にある\end{alignat*}から,上の拡張された定理は次のようになる.
〔定理 $\boldsymbol{2.\ 10}$〕 上と同じ仮定のもとにおいて,方程式\[U+\kappa V=0\]の根は $\kappa$ が実数ならば,みな実数,また $\kappa$ が虚数ならば,みな虚数で,かつ根の虚数部は $\kappa$ の虚数部と同じ符号をもつ.
さて,実根の場合に返って,方程式\[\frac{\ f(z)\ }{\overline{f}(z)}=\lambda,\hspace{1cm}|\lambda|=1\]すなわち\[\frac{\ a_0\ }{\overline{a}_0}\ \frac{\ z-\alpha_1\ }{z-\overline{\alpha}_1}\ \frac{\ z-\alpha_2\ }{z-\overline{\alpha}_2}\ \cdots\ \frac{\ z-\alpha_n\ }{z-\overline{\alpha}_n}=\lambda\]を考察する.
または因数 $\dfrac{\ a_0\ }{\overline{a}_0}$ を右辺に移して\[\frac{\ z-\alpha_1\ }{z-\overline{\alpha}_1}\ \frac{\ z-\alpha_2\ }{z-\overline{\alpha}_2}\ \cdots\ \frac{\ z-\alpha_n\ }{z-\overline{\alpha}_n}=\lambda^\prime,\tag{$\ 4\ $}\]\[\lambda^\prime=\frac{\overline{a}_0}{\ a_0\ }\lambda,\hspace{1cm}|\lambda^\prime|=1\]
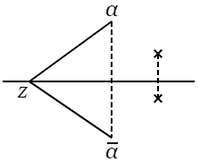 |
$z$ が実数ならば,両辺の絶対値は相等しいから,更に両辺の偏角を比較する.ただし $\operatorname{arc}\ \lambda^\prime$ はたとえば $(0,\ 2\pi)$ の間にきめておく.
$z$ が実数軸の上を $-\infty$ から $+\infty$ まで移動するときに,$\operatorname{arc}\ \left(\dfrac{z-\alpha}{z-\overline{\alpha}}\right)$ は $0$ から $2\pi$ まで単調に増大するから,$(\ 4\ )$ の左辺の $\operatorname{arc}$ は $0$ から $2n\pi$ まで単調に増大する.ゆえにこの間に $(\ 4\ )$ の両辺の $\operatorname{arc}$ の差が $2\pi$ の倍数になり,したがって等式 $(\ 4\ )$ が成り立つことが $n$ 回ある.すなわち $(\ 4\ )$ は $n$ 個の実根をもつのである.ただし $\operatorname{arc}\ (\lambda^\prime)=0$(すなわち $\lambda^\prime=1$)のときには,左辺の $\operatorname{arc}$ が $0$ または $2n\pi$ になるのは $z=\pm\infty$ のときであるから,根は $n-1$ 個になるが,そのときには方程式 $(\ 4\ )$ も $n-1$ 次になるのである.
根がみな実数であることは,しかしながら既知である.新たに知り得たことは,それらの根がみな単根であることである.
さて\[\operatorname{arc}(\lambda^\prime)=\theta,\hspace{15mm}\operatorname{arc}(\lambda_1{}^\prime)=\theta_1,\]\[0\leqq\theta\lt\theta_1\lt2\pi\]として\[F(z)\equiv{\textstyle\prod}\frac{\ z-\alpha\ }{z-\overline{\alpha}}=\lambda^\prime,\tag{$\ 5\ $}\]\[F(z)\equiv{\textstyle\prod}\frac{\ z-\alpha\ }{z-\overline{\alpha}}=\lambda_1{}^\prime,\tag{$\ 6\ $}\]を比較して考えると,$z$ が $-\infty$ から漸次増大して $z=z_1$ のとき $F(z)$ の $\operatorname{arc}$ が $\theta$ に等しくなったとすれば,$z_1$ がすなわち $(\ 5\ )$ の最小の根である.それから $z$ が更に増大するときに,初めて $\operatorname{arc}\ F(z)$ が $\theta_1$ に等しくなることがある.そのときの $z$ の値を $z_1{}^\prime$ とすれば,$z_1{}^\prime$ がすなわち $(\ 6\ )$ の最小の根である.$z$ がなお増大して,$z=z_2$ のとき $\operatorname{arc}\ F(z)$ が $\theta+2\pi$ になり,$z$ がなお増大して $z=z_2{}^\prime$ のとき $\operatorname{arc}\ F(z)$ が $\theta^\prime+2\pi$ になるとすれば,$z_2$,$z_2{}^\prime$ は大小の順序においてそれぞれ $(\ 5\ )$,$(\ 6\ )$ の第二の根で\[z_1\lt z_1{}^\prime\lt z_2\lt z_2{}^\prime.\] $z$ がなお増大するとき,このような関係が繰り返されて,$(\ 5\ )$,$(\ 6\ )$ の根が互いに隔離する.
$U(z)=0$,$V(z)=0$ は $\lambda=1$ および $\lambda=-1$ なる場合であるが,一般に $k$,$k^\prime$ を相異なる実数とするとき,\[U-kV=0 と U–k^\prime V=0\]との根が互いに隔離するのである.
$\boldsymbol{2.}$ 上の Hermite の定理の逆が次のような意味で成り立つ.
〔問題 $\boldsymbol{1}$〕 実方程式 $U(z)=0$,$V(z)=0$ の根が実数の単根のみで,かつ互いに隔離するならば,$U(z)-kV(z)=0$ の根は,$k$ が実数ならば,ことごとく実数で,$k$ の二つの相異なる値に対する二つの方程式の根は互いに相隔離する.また $k$ が虚数ならば,根はみな虚数で,しかもことごとく実数軸の一側にある.そのいずれの側にあるかは,$k$ の虚数部の符号によって定まる.
〔解〕 $U=0$ の引続いた二つの根の間では,$U$ は一定の符号をもつ.仮定によって $U=0$ の根は単根であるから,それらの根を限界とする各区間における $U$ の符号は正負交代する.また各区間内において $V$ がただ一つの単根をもつから,$U=0$ の根である $z$ の値に対する $V$ の符号は交互に正または負である.語を換えていえば,$z$ が増大しつつ $U=0$ の根を通過するとき $UV$ の符号は常に正から負,または常に負から正に変わる.いまきまりをつけるために,後の場合を考察する.他の場合には $U$ または $V$ の代わりに $-U$ または $-V$ を取って考えればよい.
また $U$ は $V$ よりも低次でないと仮定する.さもなければ $U$ と $V$ とを交換して考えればよい.よって $U$ を $n$ 次,$V$ は $n$ 次または $n-1$ 次として,$V(z)/U(z)$ を部分分数に分解して\[\frac{\ V(z)\ }{U(z)}=c_0+\frac{c_1}{\ z-x_1\ }+\frac{c_2}{\ z-x_2\ }+\cdots+\frac{c_n}{\ z-x_n\ }\]
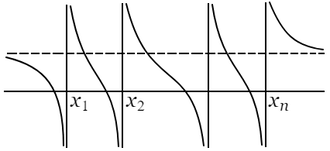 |
$x_1\lt x_2\lt\cdots\lt x_n$ として,$z$ が区間 $(x_i,\ x_{i+1})$ において増大するとすれば,$\dfrac{c_1}{\ z-x_1\ }+\cdots+\dfrac{c_i}{\ z-x_i\ }$ は正でかつ単調に減少するが,$\dfrac{c_{i+1}}{\ z-x_{i+1}\ }+\cdots+\dfrac{c_n}{\ z-x_n\ }$ は負で絶対値において単調に増大する.ゆえにこの区間において $V(z)/U(z)$ は $+\infty$ から $-\infty$ まで,単調に減少する.区間 $(-\infty,\ x_1)$ および $(x_n,\ +\infty)$ においては $c_0$ から $-\infty$ まで,または $+\infty$ から $c_0$ まで単調に減少する.
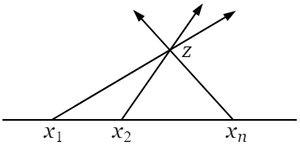
ゆえに $k$ が任意の実数であるとき,\[\frac{\ V(z)\ }{U(z)}=k\]は $(x_1,\ x_2)$,$(x_2,\ x_3)$,$\cdots$,$(x_{n-1},\ x_n)$ の各区間において一つずつの根をもち,なお $k\lt c_0$ または $k\gt c_0$ にしたがって,$(-\infty,\ x_1)$ または $(x_n,\ +\infty)$ のいずれかにおいて一つの根をもつ.$k=c_0$ ならば,$V-kU$ は $n-1$ 次になって,最後の一つの根は消失する($+\infty$ または $-\infty$ になる).
また $k$ が変わるときの根の位置の変動も明瞭である.上の図の場合では,$k$ が増せば各区間の根が単調に減少する.ただ $k$ が $y=c_0$ の線を越えるときに,一つの根が区間 $(-\infty,\ x_1)$ から $(x_n,\ +\infty)$ に飛び移るのであるが,$k$ の二つの値に対する二つの方程式の根の隔離には妨げない.
 |
また $z$ の虚数部が負ならば,$\dfrac{\ V(z)\ }{U(z)}$ の虚数部は正である.ゆえに\[U-kV=0\hspace{1cm}\left(すなわち \dfrac{\ V\ }{U}=\frac{\hphantom{1}1\hphantom{1}}{k}\right)\]の根は $k$ と同符号の虚数部をもたなければならない.
〔問題 $\boldsymbol{2}$〕 定理 $2.\ 9$ と同様に,$f(z)$ を $n$ 次の多項式とし,\[f(z)=U(z)+iV(z)\]とおくとき,$\kappa$ の虚数部が正ならば,方程式 $f(z)=0$ と $U(z)+\kappa V(z)=0$ とは実数軸の各側において同数の根をもつ.
また,$f(z)$ が実数軸の両側においてもつ根の数の差を $d$ とすれば,任意の実係数 $k$ に関して方程式 $U(z)+kV(z)=0$ は少なくとも $d$ 個の実根をもつ.
〔解〕 根の連続性(定理 $2.\ 7$)によれば簡単である.係数 $\lambda$ が $i$ から $\kappa$ まで連続的に,たとえば $i$ と $\kappa$ とを結ぶ線分上を動くとき,$U+\lambda V$ の根も連続的に変わるけれども,その間において根が実数になることはない($U$ と $V$ との共通根は初めから除いておく).ゆえに実数軸の両側にある根は各々その側においてのみ変動するから,$\lambda$ が変わっても,その数は一定である.
後段は前段を根拠にして,やはり根の連続性によって証明される.$\S\ 10$ の問題 $1$ とまったく同様である.
$f(z)$ の根が全部実数軸の一側にあるときは,上の $d$ は $n$ に等しい.すなわち Hermite の定理である.
結論だけに着眼すれば,この問題 $2$ が $\S\ 12$ の全部を被うのであるが,$\S\ 12$ の数頁が無益の逍遙であったのでもあるまい.