第 $2$ 章 方程式論の基本定理
$\S\ 13.$ Gauss の 定 理
$\boldsymbol{1.}$ 多項式 $f(z)$ とその導函数 $f^\prime(z)$ との根の複素数平面上における位置の関係に関して次の定理が成り立つ.〔定理 $\boldsymbol{2.\ 11}$〕 $f(z)=0$ の根の全部を含む凸多角形は $f^\prime(z)=0$ の根の全部を含む(Gauss の定理).
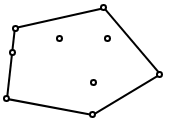 |
凸多角形はその各辺を含む直線の両側へは跨がらないから,定理を次のように変形して証明すればよい.
$f(z)=0$ の根が直線 $l$ の一側にあるときは,$f^\prime=0$ の根もその直線 $l$ の同じ側にある.
〔証〕 方程式 $f(z)=0$ の根を $\alpha$,$\beta$,$\cdots$,$\lambda$ とする.$f(z)=0$ の複根は $f^\prime(z)=0$ の根であるが,それらについては定理は当然成り立つから,$f^\prime(z)=0$ の根の中からそれらを除けば,残りの根は
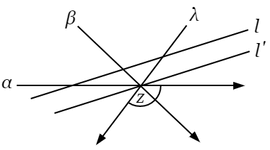 |
$z$ を通って $l$ に平行な直線 $l^\prime$ を引けば,$z-\alpha$,$z-\beta$,$\cdots$,$z-\lambda$ を表わすベクトルは $z$ を起点とするときに,$z$ に頂点をもつ二直角より小さい一つの角内に含まれる.したがって $\theta$ を適当に選んで\[\theta\lt\operatorname{arc}\ \!(z-\alpha),\hphantom{1}\operatorname{arc}\ \!(z-\beta),\ \cdots,\ \operatorname{arc}\ \!(z-\lambda)\lt\theta+\pi\]とすることができる.そうすれば\[0\gt\theta-\operatorname{arc}\ \!(z-\alpha),\hphantom{1}\theta-\operatorname{arc}\ \!(z-\beta),\ \cdots,\ \theta-\operatorname{arc}\ \!(z-\lambda)\gt-\pi.\]そこで $\varepsilon=\cos\theta+i\sin\theta$ とおけば,\[\frac{\varepsilon}{\ z-\alpha\ },\ \frac{\varepsilon}{\ z-\beta\ },\ \cdots,\ \frac{\varepsilon}{\ z-\lambda\ }\]の虚数部がことごとく負である.ゆえに\[\frac{\varepsilon}{\ z-\alpha\ }+\frac{\varepsilon}{\ z-\beta\ }+\cdots+\frac{\varepsilon}{\ z-\lambda\ }\neq0,\]すなわち\[\frac{1}{\ z-\alpha\ }+\frac{1}{\ z-\beta\ }+\cdots+\frac{1}{\ z-\lambda\ }\neq0.\]なお精密に考えるならば,$f^\prime(z)=0$ の根が直線 $l$ の上にあることができるかという問題が残っている.上の証明で,$z$ を直線 $l$ の上に取るとき,$\alpha$,$\beta$,$\cdots$,$\lambda$ の中,一つでも $l$ の上にないものがあれば,$\dfrac{\varepsilon}{\ z-\alpha\ }$,$\cdots$,$\dfrac{\varepsilon}{\ z-\lambda\ }$ の虚数部は決して正にはならず,かつ実際負になるものがあるのだから,和はやはり $0$ にならない.
すなわち $f(z)=0$ の根がことごとく一直線上にある場合を除けば,$f^\prime(z)=0$ の根は,$f(z)$ の複根であるものの外,上の凸多角形の内部にあって,その周上にあることはできないのである.
この取除けの場合は,問題として次に掲げる.
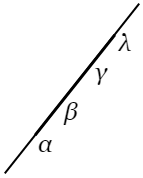
〔問題 $\boldsymbol{1}$〕 $f(z)=0$ の根が $\alpha$,$\beta$,$\gamma$,$\cdots$,$\lambda$ の順で一直線上にあるときには $f^\prime(z)=0$ の根は $f(z)$ の複根であるものの外は,その直線上 $\alpha$,$\beta$ の間,$\beta$,$\gamma$ の間等に一つずつある.すなわち $f^\prime(z)$ の根が $f(z)$ の根を隔離する.
 |
〔注意〕 一次変形によって上の直線を実数軸に変換すれば,定理は Rolle の定理からも導かれることはもちろんである($\S\ 20$).
$\boldsymbol{2.}$ 上の Gauss の定理を次のようにいってもよい.
$f(z)=0$ の根の全部を含む凸平面形は $f^\prime(z)=0$ の根の全部を含む.
このような凸平面形は,根の全部を含む最小の凸多角形を含むから,Gauss の定理を上のようにいい表わしても,定理の内容に変りはないが,応用上に都合のよい場合がしばしばある.
〔問題 $\boldsymbol{2}$〕 絶対値でいえば,$f(z)$,$f^\prime(z)$,$f^{\prime\prime}(z)$,$\cdots$ の最大根は次々に減少する.
「減少」は不増加の意味である.すなわち $f^{(k)}(z)$ の根の絶対値の最大のものを $r^{(k)}$ とすれば $r\geqq r^\prime\geqq r^{\prime\prime}\geqq\cdots\geqq r^{(k)}\geqq\cdots$.
〔解〕 上の凸平面形を $\mathrm{O}$ を中心とする円にして考えよ.
〔問題 $\boldsymbol{3}$〕 多項式 $f(x)$,$g(x)$ が実根のみをもち,かつ $f(x)$ と $g(x)$ との根が互いに隔離するときには,導函数,$f^\prime(x)$,$g^\prime(x)$ に関しても同様の関係がある.
〔解〕 Gauss の定理と Hermite の定理との組合せ.$f+ig$ の根が全部実数軸の一側にあるから,$f^\prime+ig^\prime$ の根も同様.したがって $f^\prime$,$g^\prime$ の根が互いに隔離する.$f^{\prime\prime}$,$g^{\prime\prime}$ なども同様.