第 $2$ 章 方程式論の基本定理
$\S\ 14.$ Laguerre の定理
$\boldsymbol{1.}$ 多項式\[f(x)=a_0x^n+a_1x^{n-1}+\cdots+a_kx^{n-k}+\cdots+a_n\]を斉次の形に書き表わして取り扱うのが便利な場合がしばしば生ずる.すなわち $f(x)$ の代わりに\[f(x,\ y)=a_0x^n+a_1x^{n-1}y+\cdots+a_kx^{n-k}y^k+\cdots+a_ny^n\]とするので,もとの形に返るには,$y=1$ とおくのである.$f(x,\ y)$ の $x$ および $y$ に関する導函数を $f_1$,$f_2$ で表わすときは,\[P(\xi,\ \eta\ ;\ x,\ y)\equiv\xi f_1(x,\ y)+\eta f_2(x,\ y)\]なる式は幾何学でポーラーとよぶものであるが,ここでは不斉次の形に返って,$f_1$ においても $f_2$ においても $y=1$ とおいて,同時に $\eta$ をも $1$ として,\[P(\xi,\ x)=\xi f_1(x)+f_2(x)\]をポーラーと呼ぶことにする.詳しくいえば,$P(\xi,\ x)$ は $f(x)$ に関する $\xi$ のポーラーである.たとえば,$f(x)=ax^2+2bx+c$ ならば\[\frac{1}{2}P(\xi,\ x)=\xi(ax+b)+(bx+c)\]である.
$\boldsymbol{2.}$ 方程式 $P(\xi,\ x)=0$ は $f^\prime(x)=0$ の拡張である.$P(\xi,\ x)=0$ すなわち $f_1(x)+\dfrac{1}{\xi}f_2(x)=0$ は $\xi\rightarrow\infty$ のとき $f_1(x)=0$ すなわち $f^\prime(x)=0$ になる.
この方程式 $P(\xi,\ x)=0$ に関して次の定理が成り立つ.それを $f^\prime(x)=0$ に関して前節に述べた Gauss の定理の拡張と見ることができる.
〔定理 $\boldsymbol{2.\ 12}$〕 $(\ 1\ )$ 方程式 $f(x)=0$ のすべての根を含む円を $C$ とし,$\xi$ を $C$ の外に取れば,\[P(\xi,\ x)=0\]の根はすべて円 $C$ の内にある.
$(\ 2\ )$ $\xi$ が円 $C$ の周上にあっても同様であるが,特に $f(x)=0$ の根がことごとく $C$ の周上にあるとき,$\xi$ をも $C$ の周上に取るならば,$P(\xi,\ x)=0$ の根もことごとく $C$ の周上にある.
$(\ 3\ )$ この場合に,$P(\xi,\ x)=0$ の根と $\xi$ とは $C$ の周上において $f(x)=0$ の根を隔離する.
上文において円の内部と外部とを交換しても定理は成り立つ.また直線を円周の特別の場合と見なして円の内部外部というのを直線の一側と他側とに変更しても,成り立つ.
すなわち $C$ を $\S\ 6$ に述べた円板としてよいのである.
〔証〕 $f(x)=a_0(x-\alpha)(x-\beta)\cdots(x-\lambda)$
とすれば\[f(x,\ y)=a_0(x-\alpha y)(x-\beta y)\cdots(x-\lambda y),\]\[\frac{f_1(x,\ y)}{f(x,\ y)}={\textstyle\sum}\frac{1}{\ x-\alpha y\ },\hspace{1cm}\frac{f_2(x,\ y)}{f(x,\ y)}={\textstyle\sum}\frac{-\alpha}{\ x-\alpha y\ }.\]ゆえに\[\frac{\ P(\xi,\ x)\ }{f(x)}={\textstyle\sum}\frac{\xi-\alpha}{\ x-\alpha\ },\]$\textstyle\sum$ は $\alpha$,$\beta$,$\cdots$,$\lambda$ の上にわたるのである.
ゆえに $P(\xi,\ x)$ の根($f$ と共通でないもの)は\[{\textstyle\sum}\frac{\ \xi-\alpha\ }{x-\alpha}=0\tag{$\ 1\ $}\]から求められる.いま一次変形\[x^\prime=\frac{1}{\ x-\xi\ }\tag{$\ 2\ $}\]によって問題を $x$ 平面から $x^\prime$ 平面に換えるために,\[\alpha^\prime=\frac{1}{\ \alpha-\xi\ },\hphantom{1}\beta^{\ \prime}=\frac{1}{\ \beta-\xi\ },\ \cdots,\ \lambda^\prime=\frac{1}{\ \lambda-\xi\ }\]とおけば,$(\ 1\ )$ の各項は\[\frac{\ \xi-\alpha\ }{x-\alpha}=\frac{x^\prime}{x^\prime-\alpha^\prime}\]のようになる.よって $(\ 1\ )$ は\[x^\prime{\textstyle\sum}\frac{1}{\ x^\prime-\alpha^\prime\ }=0\]になるが,$x^\prime=0$ は $x=\infty$ に対応するから,それを除けば,問題は\[{\textstyle\sum}\frac{1}{\ x^\prime-\alpha^\prime\ }=0\tag{$\ 3\ $}\]になる.さてこれは Gauss の定理 の定理で取り扱った方程式である.
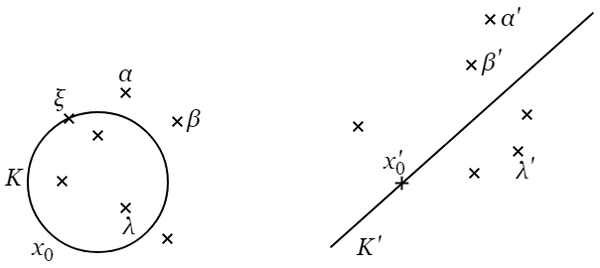 |
いま $\xi$ を任意の点,$x_0$ を $(\ 1\ )$ の一つの根とし,$\xi$ と $x_0$ とを通る任意の円周を $K$ とするならば,一次変形 $(\ 2\ )$ によって,$K$ は $x^\prime$ 平面上の一つの直線 $K^\prime$ に対応し,$x_0$ に対応する $(\ 3\ )$ の根 $x_0{}^\prime$ は $K^\prime$ の上にある.
$(\ 3\ )$ は $\alpha^\prime$,$\beta^{\ \prime}$,$\cdots$,$\lambda^\prime$ が $K^\prime$ の一側に偏在する場合には成り立ち得ないこと,Gauss の定理の証明において示したとおりである.ゆえに $\alpha^\prime$,$\beta^{\ \prime}$,$\cdots$,$\lambda^\prime$ は $K^\prime$,の両側に分配されるか,または全部が $K^\prime$ の上になければならない.$x$ 平面に返って考えるならば,$\alpha$,$\beta$,$\cdots$,$\lambda$ は $\xi$,$x_0$ を通る円 $K$ の内にも外にもなければならない,または極端の場合には,全部円 $K$ の周上になければならない.
よって $\alpha$,$\beta$,$\cdots$,$\lambda$ が円板 $C$ に属して,$\xi$ が $C$ に属さないならば,$(\ 1\ )$ の根 $x_0$ は $C$ に属さなければならない.もし,$x_0$ も $C$ に属さないと仮定するならば,$\xi$ と $x_0$ とを通ってまったく円板 $C$ の外にある円周 $K$ を作ることができて,それが$\alpha$,$\beta$,$\cdots$,$\lambda$ を分離しないことになるから,上の結果と矛盾する.
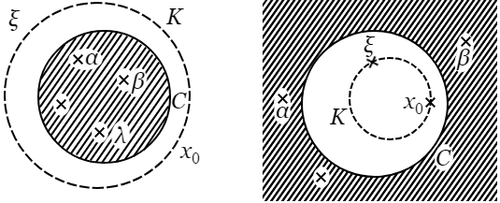 |
$\xi$ または $x_0$ が円 $C$ の周上にあるとしても同様であるが,ただ $\alpha$,$\beta$,$\cdots$,$\lambda$ が全部 $C$ の周上にある場合に,$\xi$ をも $C$ の周上に取るときだけが例外である.この場合には $\alpha^\prime$,$\beta^{\ \prime}$,$\cdots$,$\lambda^\prime$ は全部直線 $K^\prime$ の上にあるから $(\ 3\ )$ の根は $n-1$ 個の線分 $\alpha^\prime\beta^{\ \prime}$,$\beta^{\ \prime}\gamma^\prime$,$\cdots$ の上に一つずつ分配される.したがって $(\ 1\ )$ の根は $n-1$ 個の弧 $\alpha\beta$,$\beta\gamma$,$\cdots$ の上に一つずつ分配される.
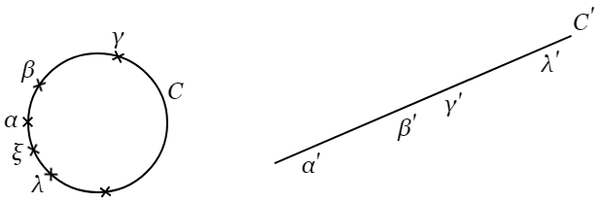 |
$f(z)=0$ の $n$ 個の根 $\alpha$,$\beta$,$\cdots$,$\lambda$ が円周 $C$ を $n$ 個の弧に分かつが,そのうち $\xi$ を含む弧(前の図)では $\lambda\alpha$ を除いた他の $n-1$ 個の弧が $(\ 1\ )$ の根を一つずつ含むのである($\xi$ は $x^\prime$ 平面の $\infty$ に対応し,弧 $\alpha\lambda$ は直線 $C^\prime$ の線分 $\alpha^\prime\lambda^\prime$ 以外の部分に対応する).
$\boldsymbol{3.}$ 等式\[\frac{\ P(\xi,\ x)\ }{f(x)}={\textstyle\sum}\frac{\ \xi-\alpha\ }{x-\alpha}\]は左辺の有理式の部分分数への分解である.ゆえに $f(z)$ の $k$ 重根は $P(\xi,\ x)$ の $k-1$ 次の根である(約分ができて分母に $x-\alpha$ なる因数が一つだけ残る).ただし $\xi$ が一つの根 $\alpha$ に合するときには,$x-\alpha$ に関する部分分数がなくなる.すなわち,このとき $x-\alpha$ が $P(\xi,\ x)$ において $f(x)$ と同次以上に含まれる.
$f(x)$ が $n$ 次ならば,$P(\xi,\ x)$ は一般には $n-1$ 次であるが,$\sum(\xi-\alpha)=0$ であるときには,$n-2$ 次以下に低下する.これを $\xi\rightarrow\dfrac{1}{n}\sum\alpha$ なる極限の場合と見なし,次数の低下が $k$ ならば,$P(\xi,\ x)$ は $\infty$ なる $k$ 次の根をもつものとする.このとき $\xi$ は根 $\alpha$,$\beta$,$\cdots$,$\lambda$ の重心であるから $\xi$ は $\alpha$,$\beta$,$\cdots$,$\lambda$ を含む円の内部にある.ゆえに $P(\xi,\ x)$ の解の中に $\infty$ が入ってもよい.
斉次の形においては次数の低下はない.ただ $x$ に関する $n-1$ 次以下の項が若干消失するだけである.たとえば\[f(x,\ y)=x^n+y^n とすれば,\ f_1=nx^{n-1},\hphantom{1}f_2=ny^{n-1}.\]ゆえに $P(0,\ x)=n$ であるが,斉次の形では\[P(0,\ \eta\ ;\ x,\ y)=n\eta y^{n-1}.\] $n$ 次の多項式 $f(x)$ に関するポーラー $P(\xi_1,\ x)$ を $x$ の多項式として $\xi_2$ のポーラーを $P(\xi_1,\ \xi_2\ ;\ x)$ とし,このようにしてついに $k$ 次のポーラー $P(\xi_1,\ \xi_2,\ \cdots,\ \xi_k\ ;\ x)$ に至れば,これは一般には $x$ に関して $n-k$ 次である.
〔問題 $\boldsymbol{1}$〕 $f(x)$ の根が全部円板 $C$ に属し,$\xi_1$,$\xi_2$,$\cdots$,$\xi_k$ が $C$ の外にあれば,$P(\xi_1,\ \xi_2,\ \cdots,\ \xi_k\ ;\ x)$ の根は $C$ に属する.
〔問題 $\boldsymbol{2}$〕 $P(\xi,\ x)$ の根($f(x)$ と共通でないもの)$x_0$ と $\xi$ とを通る任意の円は $f(x)$ の根を内外に分離する.または $f(x)$ のすべての根を通る.$P(\xi_1,\ \xi,\ \cdots,\ \xi\ ;\ x)$ に関しても同様である.
〔解〕 定理 $2.\ 12$ または問題 $1$ の対偶.
〔問題 $\boldsymbol{3}$〕 方程式\[f(z)\equiv1+z+a_2z^{\nu_2}+a_3z^{\nu_3}+\cdots+a_kz^{\nu_k}=0\tag{$\ 1\ $}\]\[(1\lt\nu_1\lt\nu_2\lt\cdots\lt\nu_k)\]は,$|z|\leqq k$ の円内に根をもつ(Fejér).
〔注意〕 初項 $1$ のほかに $k$ 個の項があって,第二項は $z$,その他の項は係数も次数も任意である.それらの係数や次数のいかんに拘わらず,根の最小絶対値が $k$ を越えないといい得るところに,この定理の興味がある.
〔解〕 根の最小絶対値を $r$ とすれば,原方程式の根は円板 $|z|\geqq r$ に属すから\[P(0,\ z)=\nu_k+(\nu_k-1)z+(\nu_k-\nu_2)a_2z^{\nu_2}+\cdots+(\nu_k-\nu_{k-1})a_{k-1}z^{\nu_{k-1}}=0\tag{$\ 2\ $}\]の根も $|z|\geqq r$ に属す.この方程式から同様にして,\[\nu_k\hspace{0.7mm}\cdotp\nu_{k-1}+(\nu_k-1)(\nu_{k-1}-1)z+\cdots+(\nu_k-\nu_{k-2})(\nu_{k-1}-\nu_{k-2})a_{k-2}z^{\nu_{k-2}}=0\tag{$\ 3\ $}\]の根も $|z|\geqq r$ に属す.しだいにこのようにして,ついに\[\nu_k\hspace{0.7mm}\cdotp\nu_{k-1}\cdots\nu_2+(\nu_{k-1}-1)\cdots(\nu_2-1)\hspace{0.7mm}\cdotp z=0\tag{$\ 4\ $}\]の根が $|z|\geqq r$ を満足させる.よって\[r\leqq\frac{\nu_k\hspace{0.7mm}\cdotp\nu_{k-1}\hspace{0.7mm}\cdotp\cdots\nu_2}{(\nu_k-1)(\nu_{k-1}-1)\cdots(\nu_2-1)}.\] さて,$\nu_k\geqq k$,$\nu_{k-1}\geqq k-1$,$\cdots$ から\[\frac{\nu_k}{\ \nu_k-1\ }\leqq\frac{k}{\ k-1\ },\hspace{1cm}\frac{\nu_{k-1}}{\ \nu_{k-1}-1\ }\leqq\frac{k-1}{\ k-2\ },\ \cdots\]したがって\[r\leqq\frac{k}{\ k-1\ }\hspace{0.7mm}\cdotp\frac{k-1}{\ k-2\ }\cdots\frac{2}{1}=k.\] $f(z)=\left(1+\dfrac{z}{k}\right)^k=1+z+\cdots$ のときには,実際 $|z|=k$ なる根があるから,上の結果において等号 $=$ が必要である.
〔問題 $\boldsymbol{4}$〕 前の問題の方程式は $0$ と $-k$ とを直径の両端とする円内に根をもつ.
〔解〕 $\xi=0$ と $(\ 2\ )$ の根とを通る円は $(\ 1\ )$ の根を含む.同様に $0$ と $(\ 3\ )$ の根とを通る円は $(\ 2\ )$ の根を含むから,$(\ 1\ )$ の根を含む.したがって,このように $0$ と $(\ 4\ )$ の根とを直径の両端とする円は $(\ 1\ )$ の根を含む.
〔問題 $\boldsymbol{5}$〕 方程式\[1+z+az^n=0\hphantom{1}(n\gt1)\]は $|z|\leqq2$ という根をもつ(Landau).また $|z+1|\leqq1$ という根をもつ(Hurwitz).等号 $=$ は,前の場合には,$1+z+\dfrac{\ z^2\ }{4}$ だけに,また後の場合には,$n=2$,$a\geqq1/4$ のときだけに限る(菅原).