第 $3$ 章 スツルムの問題$\hspace{0.5mm}$,$\hspace{-0.5mm}$根の計算
$\S\ 20.$ 根の近似的計算$\hspace{0.5mm}$,$\hspace{-0.5mm}$微分法の定理
$\boldsymbol{1.}$ 根の近似的計算は,理論上 Sturm の定理によって解決されているけれども,実際問題としては,計算の手数を節約する方法を講ずることが重要である.ここでは,その詳細に立ち入ることはできないが,標本として Newton の方法を略説する.Newton が当時新発見の微分法を応用して,方程式の近似的解法に画期的の一生面を開いたのである.まずこの方法の根拠として必要な二,三の定理から始める.それらは微分法で説明される一般的の定理であるが,ここではなるべく多項式に即して取り扱うことにする.以下本節では $f(x)$ などで表わす函数は実係数をもつ多項式とする.
$\boldsymbol{2.}$ 〔Bolzano の定理〕 区間 $a\lt x\lt b$ の両端において $f(x)$ の値が反対の符号をもつとき,$f(x)$ はこの区間内に根をもつ.
〔証〕 $a=0$,$b=1$,$f(0)\lt0$,$f(1)\gt0$ として,区間 $(0,\ 1)$ を考察する.一般の場合も同様であるが,それは $x^\prime=\dfrac{\ x-a\ }{b-a}$ なる変換によって,この場合に帰する.
区間 $(0,\ 1)$ を $10$ 分して $0$,$0.1$,$0.2$,$\cdots$,$0.9$,$1$ に対する $f(x)$ の値を次々に見て行く.もしも,それらの値の中に $0$ なるものがあるならば,問題は解決されたのである.そうでないときには,たとえば $f(0.4)\lt0$,$f(0.5)\gt0$ のように,$f(x)$ が左端では負,右端では正になる区間が必ずあるであろう.次にその区間 $(0.4,\ 0.5)$ を $10$ 分して,$0.4$,$0.41$,$\cdots$,$0.49$,$0.5$ に対する $f(x)$ の値を見れば,$f(x)$ の根が得られるか,あるいは $(0.42,\ 0.43)$ のような区間で,左端では $f(x)$ が負,右端では正になるものが得られる.このような操作を続行するならば,$0.a_1a_2\cdots a_n$ のような有限十進小数として $f(x)$ の根が得られるか,あるいは $x_0=0.a_1a_2\cdots a_n\cdots$ なる無限十進小数があって,その $\dfrac{1}{10^n}$ の位より下を切り捨て,または切り上げて得られる数を両端とする,幅が $\dfrac{1}{10^n}$ である区間の左端において $f(x)$ が負になり,右端において $f(x)$ が正になる.$n$ は随意であるから,$x_0$ を含んでいくらでも狭い区間において $f(x)$ の符号が $-$ にも $+$ にもなるのである.ゆえに多項式の連続性によって $f(x_0)=0$ である.なぜならば,もしも $f(x_0)$ がたとえば正であるとするならば,$|x-x_0|$ が十分小さい間は,$f(x)$ は正でなければならないから,それは矛盾である.
この証明は,根の近似値を求めることの可能性を示すものである.
$\boldsymbol{3.}$ 根の存在が確定した上は次の定理が得られる.
区間 $(a,\ b)$ の両端において $f(x)$ の値が同じ符号をもつか,または反対の符号をもつかにしたがって,この区間内における根の数は偶数($0$ をも入れていう)または奇数である.
実際区間内にあるすべての根を $\alpha_1$,$\alpha_2$,$\cdots$,$\alpha_k$ として\[f(x)=(x-\alpha_1)(x-\alpha_2)\cdots(x-\alpha_k)\varphi(x)\]とおけば,$\varphi(x)$ は区間 $(a,\ b)$ において根をもたない.ゆえに Bolzano の定理(対偶)によって,$\varphi(a)$,$\varphi(b)$ は同符号である.その符号を $\sigma$ とすれば $\operatorname{sign}\ \!f(a)=(-1)^k\sigma$,$\operatorname{sign}\ \!f(b)=\sigma$,すなわち $\operatorname{sign}\ \!f(a)=(-1)^k\operatorname{sign}\ \!f(b)$ である.
$\boldsymbol{4.}$ 〔Rolle の定理〕 $f(x)$ の相接する二つの根の間に $f^\prime(x)$ の根がある.
〔証〕 $a$,$b$ を $f(x)$ の相接する根とすれば,区間 $a\lt x\lt b$ において $f(x)$ は一定の符号をもつ.しかるに $x=a$ の直後では $f^\prime(x)$ は $f(x)$ と同じ符号をもち,$x=b$ の直前では $f^\prime(x)$ は $f(x)$ と反対の符号をもつ($\S\ 15$).すなわち $x=a$ の直後と $x=b$ の直前とにおいて $f^\prime(x)$ が反対の符号をもつ.ゆえに区間 $a\lt x\lt b$ において $f^\prime(x)$ が根をもたなければならない.
〔問題 $\boldsymbol{1}$〕 $f(x)$ が $m$ 個の実根をもつときには,$f^{(k)}(x)$ は $m-k$ 個以上の実根をもつ.$f(x)$ のすべての根が実根ならば,$f^{(k)}(x)$ に関しても同様で,$f^{(k-1)}(x)$ と $f^{(k)}(x)$ との根は互いに隔離する.ただし,複根は例外である.
$f(x)=a_0x^n+a_1x^{n-1}+\cdots+a_n=0$ を斉次の形\[f(x,\ y)=a_0x^n+a_1x^{n-1}y+\cdots+a_kx^{n-k}y^k+\cdots+a_ny^n=0\]に書いて,それを満足させる $\dfrac{x}{y}$ または $\dfrac{y}{x}$ の値を根と見れば,上の導函数 $f^{(k)}$ を\[\frac{\ \partial^kf(x,\ y)\ }{\partial x^\mu\partial y^\nu}\hspace{1cm}(\mu+\nu=k)\]でおき換えても同様である.
〔問題 $\boldsymbol{2}$〕 $x_1$,$x_2$,$\cdots$,$x_n$ が正数であるとき,\begin{alignat*}{1}&m_1=\frac{\ x_1+x_2+\cdots+x_n\ }{n},\\[2mm]m_2=&\sqrt{\frac{x_1x_2+x_1x_3+\cdots+x_{n-1}x_n}{\dbinom{n}{2}}}\\[2mm]&{\small\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots}\\[2mm]&m_k=\sqrt[\large k]{\varSigma x_1x_2\cdots x_k/\tbinom{n}{k}},\\[2mm]&{\small\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots}\\[2mm]&m_n=\sqrt[\large n]{x_1x_2\cdots x_n}\end{alignat*}とすれば\[m_1\geqq m_2\geqq\cdots\geqq m_k\geqq\cdots\geqq m_n\]で,どこでも,等号は $x_1=x_2=\cdots=x_n$ であるときに限って成り立つ.
$m_1$,$m_2$,$\cdots$,$m_n$ は正数 $x_1$,$x_2$,$\cdots$,$x_n$ の平均値で,$m_1$ は相加平均,$m_n$ は相乗平均である.
| 〔解〕 | \[f(x,\ y)=(x-x_1y)(x-x_2y)\cdots(x-x_ny)\] |
〔問題 $\boldsymbol{3}$〕 $c$ を任意の実数とすれば,方程式 $f(x)-cf^\prime(x)=0$ は $f(x)=0$ と同数以上の実根をもつ.
〔解〕 $F(x)=(x-c)f(x)$ として,$F^\prime(x)=f(x)-cf^\prime(x)$ を用いる.$f(x)$ の相接する二つの実根の間に $f(x)-cf^\prime(x)$ の実根が少なくとも一つずつはある.そのほか $c$ の符号によって $f(x)$ の最大実根よりも大きいまたは $f(x)$ の最小実根よりも小さい実根がある.
〔問題 $\boldsymbol{4}$〕 $b_0x^m+b_1x^{m-1}+\cdots+b_m=0$ が実根のみをもつときは,方程式\[b_0f(x)+b_1f^\prime(x)+b_2f^{\prime\prime}(x)+\cdots+b_mf^{(m)}(x)=0\]は $f(x)=0$ と同数以上の実根をもつ.
〔解〕 前の問題を反復適用する.
〔問題 $\boldsymbol{5}$〕 $f(x)=0$ は $n$ 次の方程式で,$c$ は区間 $(0,\ n)$ の外にあるときは,$cf(x)-xf^\prime(x)=0$ は $f(x)=0$ と同数以上の根をもつ.
〔解〕 問題 $3$ の証明に少しの変更を加えればできる.Laguerre は $x^{-c}f(x)$ に Rolle の定理を応用して証明した.これは微分法である.
$\boldsymbol{5.}$ 〔平均値の定理〕 区間 $(a,\ b)$ において\[\frac{\ f(b)-f(a)\ }{b-a}=f^\prime(c)\hspace{1cm}(a\lt c\lt b)\]になるような値 $c$ が存在する.
〔証〕 $x=a$,$x=b$ に対して,それぞれ $f(a)$,$f(b)$ に等しい値をもつ一次式を\[\varphi(x)=f(a)+M(x-a)\]とすれば,$M$ は\[f(b)=f(a)+M(b-a)\]から求められる.すなわち\[M=\frac{\ f(b)-f(a)\ }{b-a}.\]さて\[F(x)=f(x)-\varphi(x)\]とおけば,仮定によって $F(a)=0$,$F(b)=0$.ゆえに Rolle の定理によって $a\lt c\lt b$ なるある値に対して $F^\prime(c)=0$ になる.しかるに\[F^\prime(x)=f^\prime(x)-\varphi^\prime(x)=f^\prime(x)-M.\] ゆえに $F^\prime(c)=0$ から\[f^\prime(c)=M.\]すなわち\[f^\prime(c)=\frac{\ f(b)-f(a)\ }{b-a}\] $\boldsymbol{6.}$ これから次の定理を得る.
区間 $(a,\ b)$ において $f^\prime(x)$ が常に正「または負」ならば,$f(x)$ はこの区間において単調に増大「または減少」する.
実際 $a\lt\alpha\lt\beta\lt b$ とすれば,平均値の定理によって,\[\frac{f(\beta)-f(\alpha)\ }{\beta-\alpha}=f^\prime(c),\hspace{1cm}\alpha\lt c\lt\beta.\]仮定によって $f^\prime(c)\gt0$.ゆえに $f(\beta)\gt f(\alpha)$.
〔問題 $\boldsymbol{6}$〕 区間 $(a,\ b)$ において $f(x)$ が根をもつとき,この区間に属する $x=r$ に対して $f(r)$ の値が小さいならば,$r$ は根に近い値であろう.もしも区間 $(a,\ b)$ において,$f^\prime(x)$ が一定の符号をもち,$|f^\prime(x)|\gt m$ ならば,根を $\alpha$ とすると,\[|\alpha-r|\lt\frac{|f(r)|}{m}\] 〔解〕 $f(\alpha)-f(r)=(\alpha-r)f^\prime(c)$ から,$f(\alpha)=0$ を用いて,$-f(r)=(\alpha-r)f^\prime(c)$.$c$ は $\alpha$ と $r$ との間にあるから,$|f^\prime(c)|\gt m$.ゆえに $|f(r)|=|a-r|\ \!|f^\prime(c)|$ から,上の不等式を得る.
$\boldsymbol{7.}$ 〔平均値の定理の拡張〕 区間 $(a,\ b)$ において\[f(b)=f(a)+(b-a)f^\prime(a)+\frac{\ (b-a)^2\ }{2}f^{\prime\prime}(c),\]になるような値 $c$ が存在する.
〔証〕 $x=a$ に対して $\varphi(a)=f(a)$,$\varphi^\prime(a)=f^\prime(a)$ で,かつ $x=b$ に対して $\varphi(b)=f(b)$ になるような二次式 $\varphi(x)$ は\[\varphi(x)=f(a)+(x-a)f^\prime(a)+\frac{M}{2}(x-a)^2\]のような形である.ただし $M$ は\[f(b)=f(a)+(b-a)f^\prime(a)+M\frac{\ (b-a)^2\ }{2}\tag{$\ 1\ $}\]によって定められる定数である.
さて\[F(x)=f(x)-\varphi(x)\]とおけば,仮定によって\[F(a)=0\hspace{7mm}F^\prime(a)=0\hspace{5mm}また\hspace{5mm}F(b)=0.\] ゆえに $F^\prime(x)$ は $a$ を根とするほかに $a$,$b$ の間に根をもつ.したがって $F^{\prime\prime}(x)$ は $a$,$b$ の間に根をもつ.その根を $c$ とする.さて\[F^{\prime\prime}(x)=f^{\prime\prime}(x)-\varphi^{\prime\prime}(x)=f^{\prime\prime}(x)-M.\]ゆえに,$F^{\prime\prime}(c)=0$ から\[f^{\prime\prime}(c)=M.\]よって $(\ 1\ )$ から\[f(b)=f(a)+(b-a)f^\prime(a)+\frac{\ (b-a)^2\ }{2}f^{\prime\prime}(c).\]$c$ は $a$ と $b$ との間にあるある値であるが,$a$,$b$ の大小の関係は $a\lt b$ でも,$b\lt a$ でもよい.
$\boldsymbol{8.}$ これから次の定理を得る.
区間 $(a,\ b)$ において $f^{\prime\prime}$ が常に正「または負」ならば,$f(x)$ のグラフはこの区間において上向き「または下向き」に弯曲する.
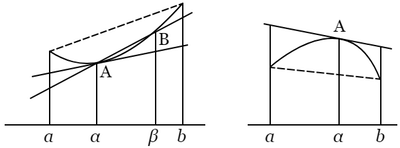 |
$x=\alpha$ に対するグラフの接線は一次式 $f(\alpha)+(x-\alpha)f^\prime(a)$ で表わされる.
さて $f(x)=\{f(\alpha)+(x-\alpha)f^\prime(\alpha)\}+\dfrac{(x-\alpha)^2}{2}f^{\prime\prime}(x^\prime)$,$x^\prime$ は $\alpha$ と $x$ との中間にあるある値であって,仮定によって $f^{\prime\prime}(x^\prime)\gt0$.ゆえにグラフは接線の上側にある(上向きの場合).
〔問題 $\boldsymbol{7}$〕 接線の代わりに点 $\mathrm{A}(\alpha,\ f(\alpha))$ と $\mathrm{B}(\beta,\ f(\beta))$ とを結ぶ弦 $\mathrm{AB}$ を取れば,区間 $(\alpha,\ \beta)$ ではグラフが $\mathrm{AB}$ の下側にあり,$(a,\ \alpha)$,$(\beta,\ b)$ では $\mathrm{AB}$ の延長の上側にある(これは上向き,$f^{\prime\prime}(x)\gt0$ の場合である.下向きの場合には,上側下側を交換する).
〔解〕 $\mathrm{AB}$ を表わす一次式を $mx+l$ とすれば $f(\alpha)=m\alpha+l$,$f(\beta)=m\beta+l$.いま $F(x)=f(x)-(mx+l)$ とおけば $F^\prime(x)=f^\prime(x)-m$,$F^{\prime\prime}(x)=f^{\prime\prime}(x)$.ゆえに $F^{\prime\prime}(x)\gt0$.
さて仮定によって $F(\alpha)=0$,$F(\beta)=0$.ゆえに $\alpha\gt\gamma\gt\beta$,$F^\prime(\gamma)=0$ とするとき,$(\alpha,\ \gamma)$ では $F^\prime(x)\lt0$,$F(x)$ は単調減少,したがって $(a,\ \alpha)$ では正,$(\alpha,\ \gamma)$ では負である.同様に,$(\gamma,\ \beta)$ では $F(x)$ は負,$(\beta,\ b)$ では正である.