第 $9$ 章 二 次 形 式
$\S\ 70.$ Gram の行列式$\hspace{0.5mm}$,$\hspace{-0.5mm}$Wronski の行列式
$\boldsymbol{1.}$ 定符号の二次形式の応用として Gram の行列式を挙げることができる.$f_1(x)$,$f_2(x)$,$\cdots$,$f_n(x)$ を区間 $a\leqq x\leqq b$ において連続な $x$ の実函数とする.もしもこの区間 $a\leqq x\leqq b$ において\[c_1f_1(x)+c_2f_2(x)+\cdots+c_nf_n(x)=0\]であるような定数 $c_1$,$c_2$,$\cdots$,$c_n$(「すべて $0$」ではない)が存在するならば,$f_1(x)$,$f_2(x)$,$\cdots$,$f_n(x)$ は区間 $a\leqq x\leqq b$ において一次的に独立でない(一次的関係をもつ)という.またそのような定数 $c_1$,$c_2$,$\cdots$,$c_n$ が存在しないならば,一次的に独立である(一次的関係をもたない)という.このような意味において,$f_1(x)$,$f_2(x)$,$\cdots$,$f_n(x)$ が一次的に独立であるか,ないかの判定条件は次のようにして求められる.いま\begin{alignat*}{1}a_{\mu\nu}=\int_a^b&f_\mu(x)f_\nu(x)dx\tag{$\ 1\ $}\\[2mm]&\!(\mu,\ \nu=1,\ 2,\ \cdots,\ n)\end{alignat*}とおけば,\begin{alignat*}{1}A(u,\ u)\equiv\int_a^b&(u_1f_1(x)+u_2f_2(x)+\cdots+u_nf_n(x))^2dx\tag{$\ 2\ $}\\[2mm]&=\underset{\mu,\ \nu}{\textstyle\sum}a_{\mu\nu}u_\mu u_\nu\hspace{1cm}(\mu,\ \nu=1,\ 2,\ \cdots,\ n)\end{alignat*}は変数 $(u)$ の二次形式である($a_{\mu\nu}=a_{\nu\mu}$).
この二次形式の判別式\[G=\begin{vmatrix}\ a_{11}&a_{12}&\cdotp&a_{1n}\ \\[1mm]\ a_{21}&a_{22}&\cdotp&a_{2n}\ \\[1mm]\ \cdotp&\cdotp&\cdotp&\cdotp\ \\[1mm]\ a_{n1}&a_{n2}&\cdotp&a_{nn}\ \end{vmatrix}\]を $f_1(x)$,$f_2(x)$,$\cdots$,$f_n(x)$ および区間 $a\leqq x\leqq b$ に関する Gram の行列式という.その組成分子 $a_{\mu\nu}$ は上の $(\ 1\ )$ の積分である.
さて二次形式 $A(u,\ u)$ は変数 $(u)$ の任意の実数値に対して,決して負の値を取らない.それは $(\ 2\ )$ からの帰結である.
$(\ 2\ )$ における被積分函数は仮定によって $x$ の連続函数で,かつ決して負にはならないのであるから,$(\ 2\ )$ が $0$ になるのは,被積分函数が積分区間 $a\leqq x\leqq b$ において常に $0$ に等しい場合に限る.
ゆえに,いま $(u)$ にある定数値 $(c)$ を与えたとするとき,\[A(c,\ c)=0\]になるのは,区間 $a\leqq x\leqq b$ において,常に\[c_1f_1(x)+c_2f_2(x)+\cdots+c_nf_n(x)=0\]であるときに限る.このような関係が $c_1=c_2=\cdots=c_n=0$ のときに限って成り立つのは,すなわち上の意味において $f_1(x)$,$f_2(x)$,$\cdots$,$f_n(x)$ が一次的に独立であるのであるが,そのときには二次形式 $A(u,\ u)$ は正の二次形式で,したがって判別式 $G\gt0$ である.
しかるにもしも $f_1(x)$,$f_2(x)$,$\cdots$,$f_n(x)$ が一次的に独立でないならば,二次形式 $A(u,\ u)$ は $u_1=u_2=\cdots=u_n=0$ 以外の $(u)$ のある値 $(c)$ に対して $0$ になるから,それは低位の二次形式でなければならない.したがって $G=0$ である.
ゆえに次の定理を得る.
〔定理 $\boldsymbol{9.\ 15}$〕 区間 $a\leqq x\leqq b$ において連続函数 $f_1(x)$,$f_2(x)$,$\cdots$,$f_n(x)$ の間に一次的関係があるために必要かつ十分な条件は,Gram の行列式が $0$ に等しいことである.すなわち\[G=0.\] ($G$ は常に $\geqq0$.ゆえに $G\gt0$ は $f_1$,$f_2$,$\cdots$,$f_n$ が $a\leqq x\leqq b$ において一次的に独立であることの条件である).
$\boldsymbol{2.}$ $f_1(x)$,$\cdots$,$f_n(x)$ は $n-1$ 回まで微分可能であるとすれば,それらの連続函数が区間 $a\leqq x\leqq b$ において一次的に独立でなくて\[c_1f_1(x)+c_2f_2(x)+\cdots+c_nf_n(x)=0\]のような関係が成り立つとき,\begin{alignat*}{1}&c_1f_1{}^\prime(x)+c_2f_2{}^\prime(x)+\cdots\cdots\cdots\cdots\cdots+c_nf_n{}^\prime(x)=0,\\[2mm]&\hphantom{c_1f_1}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\\[2mm]&c_1f_1{}^{(n-1)}(x)+c_2f_2{}^{(n-1)}(x)+\cdots+c_nf_n{}^{(n-1)}(x)=0.\end{alignat*} $c_1=c_2=\cdots=c_n=0$ でなくて,このような関係が区間 $a\leqq x\leqq b$ において成り立つから(定理 $8.\ 9$),\[W(f_1,\ f_2,\ \cdots,\ f_n)=\left|\begin{array}{llll}\ f_1(x)&f_2(x)&\cdotp&f_n(x)\ \\[1mm]\ f_1{}^\prime(x)&f_2{}^\prime(x)&\cdotp&f_n{}^\prime(x)\ \\[1mm]\ \hphantom{f_1}\cdotp&\hphantom{f}\cdotp&\cdotp&\hphantom{f_n{}^\prime(}\cdotp\ \\[1mm]\ f_1{}^{(n-1)}(x)&f_2{}^{(n-1)}(x)&\cdotp&f_n{}^{(n-1)}(x)\ \end{array}\right|=0.\] このような行列式 $W(f_1,\ f_2,\ \cdots,\ f_n)$ を $f_1(x)$,$f_2(x)$,$\cdots$,$f_n(x)$ に関する Wronski の行列式という.
すなわち $f_1(x)$,$f_2(x)$,$\cdots$,$f_n(x)$ が微分可能の条件のもとにおいて,区間で一次的に独立でないためには,この区間において,常に\[W(f_1,\ f_2,\ \cdots,\ f_n)=0\]であることが必要である.
しからば,これは十分な条件であるか.
区間 $a\leqq x\leqq b$(それを $\mathrm{I}$ と名づける)において常に\[W(f_1,\ f_2,\ \cdots,\ f_n)=0\tag{$\ 1\ $}\]であると仮定する.
なおこの区間において,常に\[W(f_1,\ f_2,\ \cdots,\ f_{n-1})\neq0\tag{$\ 2\ $}\]と仮定すれば,方程式\[\left.\begin{alignat*}{1}&K_1f_1\hphantom{^{(n-2)}}+K_2f_2\hphantom{^{(n-2)}}+\cdots+K_{n-1}f_{n-1}\hphantom{^{2)}}=f_n,\\[2mm]&K_1f_1{}^\prime\hphantom{^{n-2)}}+K_2f_2{}^\prime\hphantom{^{n-2)}}+\cdots+K_{n-1}f^\prime{}_{n-1}\hphantom{^{)}}=f_n{}^\prime,\\[2mm]&\hphantom{K}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\\[2mm]&K_1f_1{}^{(n-2)}+K_2f_2{}^{(n-2)}+\cdots+K_{n-1}f_{n-1}^{(n-2)}=f_n^{(n-2)}\end{alignat*}\ \right\}\tag{$\ 3\ $}\]から,Cramer の法則によって,区間 $\mathrm{I}$ において連続的な $x$ の函数 $K_1$,$K_2$,$\cdots$,$K_{n-1}$ が決定される.これらは $(\ 2\ )$ を分母とし,分子はそれぞれ $(\ 2\ )$ において $f_1$,$f_2$,$\cdots$,$f_{n-1}$ およびその $n-2$ 次までの導函数を $f_n$ およびその導函数でおき換えた行列式に等しい.さて仮定によって $f_1$,$f_2$,$\cdots$,$f_n$ の $n-1$ 次の導函数が可能であるから,$K_1$,$K_2$,$\cdots$,$K_{n-1}$ は微分可能である.
よって $(\ 3\ )$ の第一式から
$K_1{}^\prime f_1+K_2{}^\prime f_2+\cdots+K^\prime{}_{n-1}f_{n-1}+(K_1f_1{}^\prime+K_2f_2{}^\prime+\cdots+K_{n-1}f^\prime{}_{n-1})=f_n{}^\prime$ これを $(\ 3\ )$ の第二式と比較して
| $K_1{}^\prime f_1+K_2{}^\prime f_2+\ \cdots\ +K^\prime{}_{n-1}f_{n-1}=0,$ | ||
| 同様に | $K_1{}^\prime f_1{}^\prime+K_2{}^\prime f_2{}^\prime+\cdots+K^\prime{}_{n-1}f^\prime{}_{n-1}=0,$ | |
| $\cdotp\hphantom{f_1+K}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp\hphantom{nn}$ | ||
| $K_1{}^\prime f_1^{(n-2)}+K_2{}^\prime f_2^{(n-2)}+\cdots+K^\prime{}_{n-1}f_{n-1}^{(n-2)}=0.$ |
よって $(\ 2\ )$ から(定理 $8.\ 9$)\[K_1{}^\prime=K_2{}^\prime=\cdots=K^\prime{}_{n-1}=0.\]すなわち $K_1$,$K_2$,$\cdots$,$K_{n-1}$ は定数である.
これらの定数の中に $0$ に等しくないものがあるならば,$(\ 3\ )$ の第一式によって $f_1$,$f_2$,$\cdots$,$f_n$ の間に一次的関係があるのであるが,もしまた $K_1$,$K_2\cdots$,$K_{n-1}$ は全部 $0$ に等しいならば,$f_n$ は区間 $\mathrm{I}$ において常に $0$ に等しいのである.この場合にも,$f_1$,$f_2$,$\cdots$,$f_n$ の間に一次的関係があるといってよい.$C_1f_1+C_2f_2+\cdots+C_nf_n=0$ が $C_1=C_2=\cdots=C_{n-1}=0$,$C_n\neq0$ として成り立つからである.
上記は $(\ 2\ )$ という仮定からの帰結である.もしも $(\ 2\ )$ が成り立たないで,区間 $\mathrm{I}$ における $x$ のある値 $x=x_0$ に対して\[W(f_1,\ f_2,\ \cdots,\ f_{n-1})=0\]であるときには,区間 $\mathrm{I}$ において $f_1$,$f_2$,$\cdots$,$f_n$ の間に一次的の関係があると断言することができない.
簡単のために $W(f_1,\ f_2,\ \cdots,\ f_{n-1})$ は $x=x_0$ において $0$ になるほかは区間 $a\leqq x\leqq b$ において決して $0$ にならないとして見よう.
しからば,上の通り $f_1$,$f_2$,$\cdots$,$f_n$ の間には $a\leqq x\leqq x_0$ において\[C_1f_1+C_2f_2+\cdots+C_nf_n=0,\]また $x_0\leqq x\leqq b$ において\[C_1{}^\prime f_1+C_2{}^\prime f_2+\cdots+C_n{}^\prime f_n=0\]のような関係があるが,もしも定数因子 $C_1$,$C_2$,$\cdots$,$C_n$ と $C_1{}^\prime$,$C_2{}^\prime$,$\cdots$,$C_n{}^\prime$ とが互いに比例しないならば,これは区間 $\mathrm{I}$ における $f_1$,$f_2$,$\cdots$,$f_n$ の間の一次的関係とはいわれない.定数因子が $x_0$ の左右である二つの小区間において同一でないことは可能である.たとえば,行列\[\left(\begin{array}{llll}f_1(x_0)&f_2(x_0)&\cdotp\hphantom{nn}\cdotp&f_{n-1}(x_0)\\[1mm]f_1{}^\prime(x_0)&f_2{}^\prime(x_0)&\cdotp\hphantom{nn}\cdotp&f^\prime{}_{n-1}(x_0)\\[1mm]\hphantom{f_1}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp&\hphantom{f}\cdotp\hphantom{nn}\cdotp\hphantom{nn}\cdotp&\cdotp\hphantom{nn}\cdotp&\hphantom{f^\prime}\cdotp\hphantom{nn}\cdotp\\[1mm]f_1{}^{(n-2)}(x_0)&f_2{}^{(n-2)}(x)_0&\cdotp\hphantom{nn}\cdotp&f_{n-1}^{(n-2)}(x_0)\\[1mm]f_1{}^{(n-1)}(x_0)&f_2{}^{(n-1)}(x_0)&\cdotp\hphantom{nn}\cdotp&f_{n-1}^{(n-1)}(x_0)\end{array}\right)\]の位が $n-1$ より小さいときには,$\lambda_1=\lambda_2=\cdots=\lambda_{n-1}=0$ 以外に\begin{alignat*}{1}&\lambda_1f_1(x_0)\hphantom{^{(n-1)}}+\lambda_2f_2(x_0)\hphantom{^{(n-1)}}+\cdots+\lambda_{n-1}f_{n-1}(x_0)=0,\\[2mm]&\lambda_1f_1{}^\prime(x_0)\hphantom{^{n-1)}}+\lambda_2f_2{}^\prime(x_0)\hphantom{^{n-1)}}+\cdots+\lambda_{n-1}f^\prime{}_{n-1}(x_0)=0,\\[2mm]&\hphantom{\lambda_1}\cdotp\hphantom{M}\cdotp\hphantom{M}\cdotp\hphantom{M}\cdotp\hphantom{M}\cdotp\hphantom{M}\cdotp\hphantom{M}\cdotp\hphantom{M}\cdotp\hphantom{M}\cdotp\hphantom{M}\cdotp\hphantom{M}\cdotp\hphantom{M}\cdotp\hphantom{M}\cdotp\hphantom{M}\cdotp\\[2mm]&\lambda_1f_1{}^{(n-1)}(x_0)+\lambda_2f_2{}^{(n-1)}(x_0)+\cdots+\lambda_{n-1}f^{(n-1)}(x_0)=0\end{alignat*}なる定数がある.よって\[\lambda_1=c_1-c_1{}^\prime,\hphantom{m}\lambda_2=c_2-c_2{}^\prime,\ \cdots,\ \lambda_{n-1}=c_{n-1}-c^\prime{}_{n-1}\]として,\begin{alignat*}{1}&a\leqq x\leqq x_0\ \style{font-family:serif}{\text{では}}\ f_n(x)=c_1f_1(x)+c_2f_2(x)+\cdots+c_{n-1}f_{n-1}(x)\\[2mm]&x_0\leqq x\leqq b\ \style{font-family:serif}{\text{では}}\ f_n(x)=c_1{}^\prime f_1(x)+c_2{}^\prime f_2(x)+\cdots+c^\prime{}_{n-1}f_{n-1}(x)\end{alignat*}とおくならば,$f_n(x)$ は $x=x_0$ においても連続でかつ $x=x_0$ において $f_n(x)$ が $n-1$ 回まで微分可能で全区間 $\mathrm{I}$ において $W(f_1,\ f_2,\ \cdots,\ f_n)=0$ である.
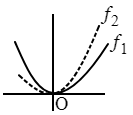 |
$W(f_1,\ f_2,\ \cdots,\ f_n)=0$ なる仮定のもとにおいて $x=x_0$ なる一つの点で\[W(f_1,\ f_2,\ \cdots,\ f_{n-1})\neq0\tag{$\ 4\ $}\]ならば,連続性のために $x_0$ を含むある区間 $I_0$ において,$(\ 4\ )$ が常に成り立ち,したがってその区間内においては $f_1$,$f_2$,$\cdots$,$f_n$ の間に一次的関係\[C_1f_1+C_2f_2+\cdots+C_nf_n=0\]が確かに成り立つ.よってもしも $f_1$,$f_2$,$\cdots$,$f_n$ が解析的函数であるならば,この一次的関係はそれらの解析的函数の全成立範囲において成り立つ.ゆえに解析的函数 $f_1(x)$,$f_2(x)$,$\cdots$,$f_n(x)$ に関しては,次の簡明な結論を得る.
ある区間において,解析的函数 $f_1(x)$,$f_2(x)$,$\cdots$,$f_n(x)$ に関する Wronski の行列式 $W(f_1,\ f_2,\ \cdots,\ f_n)$ が常に $0$ ならば,それらの函数の成立範囲を通じて,上のような一次的関係が成り立つ.
もしもすでに $W(f_1,\ f_2,\ \cdots,\ f_{n-1})=0$ ならば,$f_n(x)$ を除外して考えるのである.
(一次的関係の定義が $n$ 個の函数全部が実際に参加することを要求していないことに注意することを要する).