第 $1$ 章 初 等 整 数 論
$\S\ 13.$ 平方剰余の相互法則
$\boldsymbol{1.}$ 与えられた数 $m$ がいかなる素数 $p$ の平方剰余であるか,また非剰余であるか.この問題は古典的整数論において基本的である.
〔定理 $\boldsymbol{1.\ 33}$〕 $\boldsymbol{p}$,$\boldsymbol{q}$ を相異なる奇数の素数とすれば,\[\boldsymbol{\left(\frac{p}{q}\right)\left(\frac{q}{p}\right)=\left(-1\right)^{\displaystyle\small\raise{0.5em}{\frac{p-1}{2}\hspace{0.7mm}\cdotp\frac{q-1}{2}}},}\tag{$\ 1\ $}\]\[\boldsymbol{\left(\frac{-1}{p}\right)=\left(-1\right)^{\displaystyle\small\raise{0.5em}\frac{p-1}{2}},}\tag{$\ 2\ $}\]\[\boldsymbol{\left(\frac{2}{p}\right)=\left(-1\right)^{\displaystyle\small\raise{0.5em}\frac{p^2-1}{8}},}\tag{$\ 3\ $}\] $\left(\ 1\ \right)$ を平方剰余の相互法則,$\left(\ 2\ \right)$ をその第一補充法則,$\left(\ 3\ \right)$ を第二補充法則という.
〔注意〕 まず法則の意味を説明する.
奇数 $m$ が $4n+1$ の形かまたは $4n-1$ の形かであるに従って,$\left(m-1\right)/2$ は偶数または奇数である.実際\[\frac{\left(4n+1\right)-1}{2}=2n,\hphantom{m}\frac{\left(4n-1\right)-1}{2}=2n-1.\] 故に $\left(\ 1\ \right)$ の意味は次の通りである.
$p$,$q$ のうち少なくとも一つが $4n+1$ の形の素数ならば,$\left(\dfrac{p}{q}\right)$ と $\left(\dfrac{q}{p}\right)$ とはともに $+1$ またはともに $-1$ で,すなわち相等しい.$p$ も $q$ も $4n-1$ の形の素数であるときに限って,$\left(\dfrac{p}{q}\right)=-\left(\dfrac{q}{p}\right)$.
また $\left(\ 2\ \right)$ の意味は次の通りである.
$p$ が $4n+1$ の形か,または $4n-1$ の形かの素数であるに従って,$\left(\dfrac{-1}{p}\right)$ は $+1$ または $-1$ である.すなわち合同式 $x^2\equiv-1\hphantom{m}\left(\text{mod}.\ p\right)$ に解があるために必要かつ十分な条件は $p\equiv1\hphantom{m}\left(\text{mod}.\ 4\right)$.
さて $\left(\ 3\ \right)$ であるが,すべて奇数 $m$ は $8n\pm1$ または $8n\pm5$ の形の数である.これらの二つの場合において,それぞれ $\left(m^2-1\right)/8$ は偶数または奇数である.
実際\begin{alignat*}{2}\frac{\left(8n\pm1\right)^2-1}{8}&=8n^2\pm2n&\hphantom{m}&(偶数),\\[2mm]\frac{\left(8n\pm5\right)^2-1}{8}&=8n^2\pm10n+3&\hphantom{m}&(奇数).\end{alignat*} 故に $\left(\ 3\ \right)$ の意味は次の通りである.
$p$ が $8n\pm1$ の形か,または $8n\pm5$ の形かの素数であるに従って,$\left(\dfrac{2}{p}\right)$ は $+1$ または $-1$ である.すなわち合同式 $x^2\equiv2\hphantom{m}\left(\text{mod}.\ p\right)$ に解があるために必要かつ十分な条件は $p\equiv\pm1\hphantom{m}\left(\text{mod}.\ 8\right)$.
$\left(\ 1\ \right)$ はすでに Euler が帰納的に発見したもので,Legendre はそれを上記のような形式に書き表わし,かつその証明を試みたのであるが,かれはその証明において,算術級数中に素数の存在することを証明なしに仮定したから,その証明は完全ということを得なかった.相互法則の最初の完全なる証明は Gauss の功績に帰する.Gauss は相互法則を整数論の基本定理と名づけ,六つの全く趣を異にする証明を与えた.
次に掲げるのは,相互法則の多くの証明の中で,最も簡明なものである.この証明は実質的には,Gauss の第三証明と同一で,平方剰余に関する Gauss の予備定理と称されるものを根拠とする.それは Euler の規準(定理 $1.\ 32$)の変形である.
〔Gauss の予備定理〕 $a$ が $p$ で割り切れないならば,\[1\hspace{0.7mm}\cdotp a,\ \ 2\hspace{0.7mm}\cdotp a,\ \ 3\hspace{0.7mm}\cdotp a,\ \cdots\cdots,\ \frac{p-1}{2}\ a\tag{$\ 4\ $}\]を $p$ で割るときの剰余の中に $p/2$ よりも大きいものが $n$ 個あるとすれば,\[\left(\frac{a}{p}\right)=\left(-1\right)^n.\] 〔証〕 或る数を $p$ で割った剰余が $p/2$ よりも大きいならば,それから $p$ を引けば,絶対値において $p/2$ よりも小さい負の剰余を得る.いわゆる絶対的最小剰余である.よって上記の $n$ は $\left(\ 4\ \right)$ の数を $p$ で割るときの絶対的最小剰余の中で負になるものの数である.
$p$ を法としての $\left(\ 4\ \right)$ の数の絶対的最小剰余は $\pm1$,$\pm2$,$\cdots\cdots$,$\pm\left(p-1\right)/2$ の中にあるが,$\left(\ 4\ \right)$ の数の中のどの二つの差も,和も $p$ では割り切れないから,絶対的最小剰余として相等しいものはもちろん,符号だけが反対なものも出てこない.すなわち全体としていえば,絶対的最小剰余は,絶対値においては $1$,$2$,$\cdots\cdots$,$\left(p-1\right)/2$ に等しくて,そのうちいくつかが負になる.その負になるものの数を $n$ とするのである.よって\[1a\hspace{0.7mm}\cdotp2a\hspace{0.7mm}\cdotp\cdots\cdots\frac{p-1}{2}a\equiv\left(-1\right)^n\hspace{0.7mm}\cdotp1\hspace{0.7mm}\cdotp2\hspace{0.7mm}\cdotp\cdots\cdots\frac{p-1}{2}\hphantom{m}\left(\text{mod}.\ p\right),\]すなわち\[a^{\displaystyle\small\raise{0.5em}\frac{p-1}{2}}\equiv\left(-1\right)^n\hphantom{m}\left(\text{mod}.\ p\right).\]故に Euler の規準によって\[\left(\frac{a}{p}\right)\equiv\left(-1\right)^n\hphantom{m}\left(\text{mod}.\ p\right).\]$\left(\dfrac{a}{p}\right)$ も $\left(-1\right)^n$ も $\pm1$ に等しく,$p$ は奇数であるから,\[\left(\frac{a}{p}\right)=\left(-1\right)^n.\]
さて定理 $1.\ 33$ の証明を始める.
第一補充法則 $\left(\ 2\ \right)$ は Euler の規準(定理 $1.\ 32$)からただちに出る.\[\left(\frac{-1}{p}\right)\equiv\left(-1\right)^{\displaystyle\small\raise{0.5em}\frac{p-1}{2}}\hphantom{m}\left(\text{mod}.\ p\right).\]$p$ は奇数であるから,\[\left(\frac{-1}{p}\right)=\left(-1\right)^{\displaystyle\small\raise{0.5em}\frac{p-1}{2}}.\] または Gauss の予備定理によるならば,この場合,$a=-1$ であるから,$\left(\ 4\ \right)$ の数は\[-1,\ -2,\ \cdots\cdots,\ -\frac{p-1}{2}\]で,これらは全部 $p$ を法としての絶対的最小剰余であるから,$n=\left(p-1\right)/2$.したがって\[\left(\frac{-1}{p}\right)=\left(-1\right)^{\displaystyle\small\raise{0.5em}\frac{p-1}{2}}.\] 第二補充法則 $\left(\ 3\ \right)$ の場合には,$\left(\ 4\ \right)$ の数は($a=2$)\[2,\ \ 4,\ \ 6,\ \cdots\cdots,\ \ p-5,\ \ p-3,\ \ p-1.\]この中 $p/2$ より大きいものの数が $n$ である.故に $n$ は奇数 $1$,$3$,$5$,$\cdots\cdots$ の中で $p/2$ よりも小さいものの数である.それを数えるのは困難ではないが,面倒である.しかるにわれわれの目的は $n$ が偶数であるか,奇数であるかを知るにあるから,\[n\equiv1+3+5+\cdots\cdots\hphantom{m}\left(\text{mod}.\ 2\right)\]としてよろしい.ただし右辺の和は $p/2$ よりも小さいすべての奇数の上にわたるのである.この和の末項が $\left(p-1\right)/2$ であるか,ないかを確かめるまでもなく,$2$ が法であるから,\[n\equiv1+2+3+4+5+\cdots\cdots+\frac{p-1}{2}\hphantom{m}\left(\text{mod}.\ 2\right),\]すなわち\[n\equiv\frac{1}{2}\hspace{0.7mm}\cdotp\frac{p-1}{2}\left(\frac{p-1}{2}+1\right)=\frac{p^2-1}{8}\hphantom{m}\left(\text{mod}.\ 2\right).\] すなわち $\left(\ 3\ \right)$ が証明されたのである.
| $\ ^*\ $ | 東京数学物理学会記事 ($1904$). |
平面上にそれぞれ一定の距離を置いて二組の平行線を引いて,その平面を合同な平行四辺形の網をもって被うとき,このような図形を格子といい,それらの平行線の交叉する点を格子点という.
ここでは,その平行四辺形を正方形(方眼)とする.一つの方眼の二辺を直角座標の軸にとって,方眼の幅を $1$ とすれば,格子点は座標 $x$,$y$ がともに整数である点である.
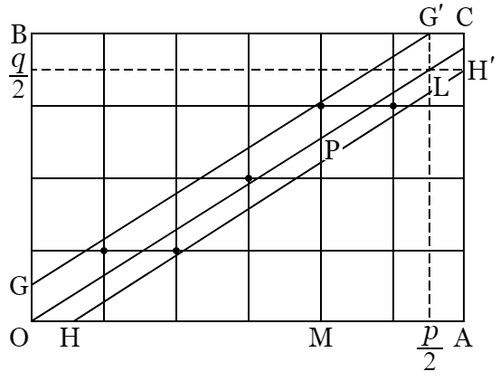 |
上の図の正方格子において $x$ 軸上に $\mathrm{OA}=\left(p+1\right)/2$ を,また $y$ 軸上に $\mathrm{OB}=\left(q+1\right)/2$ をとって長方形 $\mathrm{OACB}$ の内部の格子点を考察する.いま,直線 $\dfrac{y}{x}=\dfrac{q}{p}$ を $\mathrm{OL}$ とする.横線 $\mathrm{OM}=x$ に対応する $\mathrm{OL}$ 上の点を $\mathrm{P}$ とすれば,縦線 $\mathrm{MP}=qx/p$.
故に $x$ を $1$,$2$,$\cdots\cdots$,$\left(p-1\right)/2$ とするとき,$qx$ を $p$ で割った剰余が $p/2$ よりも大きいのは,$qx/p$ の分数部分が $1/2$ よりも大きいときで,すなわち $\mathrm{P}$ を通る縦線上で $\mathrm{P}$ から $1/2$ 以内の距離にある格子点が $\mathrm{OL}$ の上側にあるときに限る.故に $\left(\dfrac{q}{p}\right)=\left(-1\right)^n$ における $n$ は $\mathrm{OL}$ とそれを $y$ 軸の向きに $1/2$ だけ平行に移動した $\mathrm{GG}^\prime$ とにはさまれる平行四辺形 $\mathrm{OGG}^\prime\mathrm{L}$ の内部にある格子点の数である.
同様に $\left(\dfrac{p}{q}\right)=\left(-1\right)^m$ における $m$ は $\mathrm{OL}$ とそれを $x$ 軸の向きに $1/2$ だけ平行に移動した $\mathrm{HH}^\prime$ とにはさまれる平行四辺形 $\mathrm{OHH}^\prime\mathrm{L}$ の内部にある格子点の数である.
すなわち $\left(\dfrac{p}{q}\right)\left(\dfrac{q}{p}\right)=\left(-1\right)^{m+n}$ における $m+n$ はこれら二つの平行四辺形の内部にある格子点の総数であるが,図に示すように格子点 $\mathrm{C}(\ \!(p+1)/2,\ (q+1)/2)$ を一頂点とする,一辺が $1/2$ である小正方形 $\mathrm{CG}^\prime\mathrm{LH}^\prime$ を付け加えて六角形 $\mathrm{OGG}^\prime\mathrm{CH}^\prime\mathrm{H}$ を作れば,その内部における格子点の数はやはり $m+n$ である.
さて $\mathrm{OC}$ の中点 $(\ \!(p+1)/4,\ (q+1)/4)$ はこの六角形の対称の中心で,格子点はこの点に関して二つずつ互いに対称であることは作図によって明白である.故に $m+n$ が奇数であるか,偶数であるかは,中心 $(\ \!(p+1)/4,\ (q+1)/4)$ それ自身が格子点であるか,または格子点でないかによって決定される.
故に $(p+1)/4$,$(q+1)/4$ がともに整数,すなわち $p$,$q$ がともに $4t-1$ の形の素数であるときに限って,$m+n$ は奇数,したがって\[\left(\frac{p}{q}\right)\left(\frac{q}{p}\right)=-1\]である.すなわち $\left(\ 1\ \right)$ は証明された.
あるいはまた三角形 $\mathrm{GG}^\prime\mathrm{B}$,$\mathrm{HH}^\prime\mathrm{A}$ は同数の格子点を含むから,それを $k$ とすれば,長方形 $\mathrm{OACB}$ の内部の格子点の総数は $m+n+2k$ である.しかるに長方形の内部には明らかに\[\frac{p-1}{2}\hspace{0.7mm}\cdotp\frac{q-1}{2}\]の格子点があるから\[\left(\frac{p}{q}\right)\left(\frac{q}{p}\right)=\left(-1\right)^{m+n}=\left(-1\right)^{m+n+2k}=\left(-1\right)^{\displaystyle\small\raise{0.5em}{\frac{p-1}{2}\hspace{0.7mm}\cdotp\frac{q-1}{2}}}.\] 〔問題 $\boldsymbol{1}$〕 $p$ が $8n+1$ または $8n+3$ の形の素数であるときに限って\[\left(\frac{-2}{p}\right)=1.\]
| 〔解〕 | \[\left(\frac{-2}{p}\right)=\left(\frac{-1}{p}\right)\left(\frac{2}{p}\right)=\left(-1\right)^{\displaystyle\small\raise{0.5em}{\frac{p-1}{2}+\frac{p^2-1}{8}}}.\] |
| 〔解〕 | \[\left(\frac{5}{p}\right)=\left(\frac{\raise{0.1em}p}{\lower{0.1em}5}\right).\] |
| 〔解〕 | \[\left(\frac{3}{p}\right)=\left(-1\right)^{\displaystyle\small\raise{0.5em}\frac{p-1}{2}}\left(\frac{\raise{0.1em}p}{\lower{0.1em}3}\right).\] |
| $\lower{0.1em}{\text{mod}.\ 4}$ | $\lower{0.1em}{\text{mod}.\ 3}$ | $\lower{0.1em}{\text{mod}.\ 12}$ | $\raise{0.6em}{\left(-1\right)^{\displaystyle\small\raise{0.3em}\frac{p-1}{2}}}$ | $\left(\dfrac{\raise{0.1em}p}{\lower{0.1em}3}\right)$ | $\left(\dfrac{3}{p}\right)$ | |||||||
| $p\equiv\left\{\begin{array}{c}\hphantom{-}1\\-1\\\hphantom{-}1\\-1\end{array}\right.$ | $\begin{array}{c}\hphantom{-}1\\-1\\-1\\\hphantom{-}1\end{array}$ | $\begin{array}{c}\hphantom{-}1\\-1\\\hphantom{-}5\\-5\end{array}$ | $\begin{array}{c}+1\\-1\\+1\\-1\end{array}$ | $\begin{array}{c}+1\\-1\\-1\\+1\end{array}$ | $\begin{array}{c}+1\\+1\\-1\\-1\end{array}$ | |||||||
相互法則を応用して $p$,$a$ が与えられたとき $\left(\dfrac{a}{p}\right)$ の値を計算することができる.
| 〔例 $1$〕 | $\begin{alignat*}{2}\left(\frac{17}{23}\right)&=\left(\frac{23}{17}\right)&\hspace{1cm}&17\equiv1\hphantom{1}\left(\text{mod}.\ 4\right)\\&=\left(\frac{6}{17}\right)&\hspace{1cm}&23\equiv6\hphantom{1}\left(\text{mod}.\ 17\right)\\&=\left(\frac{2}{17}\right)\left(\frac{3}{17}\right)&\hspace{1cm}&\left(\cssId{eq1}{定理\ 1.\ 31}\right)\\&=\left(+1\right)\left(\frac{3}{17}\right)&\hspace{1cm}&\left(第二補充法則\right)\\&=\left(\frac{17}{3}\right)=\left(\frac{2}{3}\right)&\hspace{1cm}&17\equiv2\hphantom{1}\left(\text{mod}.\ 3\right)\\&=-1.&\hspace{1cm}&\left(第二補充法則\right)\\\end{alignat*}$ |
| 〔例 $2$〕 | $\begin{alignat*}{2}\left(\frac{365}{1847}\right)&=\left(\frac{5}{1847}\right)\left(\frac{73}{1847}\right)&\hspace{1cm}&365=5\times73\\&=\left(\frac{1847}{5}\right)\left(\frac{1847}{73}\right)&\hspace{1cm}&5\equiv1,\ \ 73\equiv1\hphantom{1}\left(\text{mod}.\ 4\right)\\&=\left(\frac{2}{5}\right)\left(\frac{22}{73}\right)&\hspace{1cm}&1847\equiv2\hphantom{1}\left(\text{mod}.\ 5\right)\ \equiv22\hphantom{1}\left(\text{mod}.\ 73\right)\\&=\left(\frac{2}{5}\right)\left(\frac{2}{73}\right)\left(\frac{11}{73}\right)&&\\&=-\left(\frac{11}{73}\right)&\hspace{2cm}&\left(第二補充法則\right)\\&=-\left(\frac{73}{11}\right)=-\left(\frac{-4}{11}\right)&\hspace{1cm}&73\equiv-4\hphantom{1}\left(\text{mod}.\ 11\right)\\&=-\left(\frac{-1}{11}\right)\left(\frac{2^2}{11}\right)=-\left(\frac{-1}{11}\right)&&\\&=+1&\hspace{2cm}&\left(第一補充法則\right)\end{alignat*}$ |
一層簡便な計算法を $\S\ 14$ に掲げる.