第 $4$ 章 二次体 $K\left(i\right)$,$K\left(\sqrt{-3}\right)$ の整数
$\S\ 39.$ 二次体 $\boldsymbol{K\left(\sqrt{-3}\right)}$ の整数
$\boldsymbol{1.}$ 本節では $1$ の三乗根を $\omega$ で表わし\[\omega=\frac{-1+\sqrt{-3}}{2},\hphantom{m}\overline{\omega}=\omega^2=\frac{-1-\sqrt{-3}}{2}\]とする.$x$,$y$ を有理数とすれば\[x+y\omega\tag{$\ 1\ $}\]のような数からは四則によって同様の数のみが生ずる.和および差に関しては論はないが,積は\begin{alignat*}{1}\left(x+y\omega\right)\left(x^\prime+y^\prime\omega\right)&=xx^\prime+\left(xy^\prime+x^\prime y\right)\omega+yy^\prime\omega^2\\[2mm]&=\left(xx^\prime-yy^\prime\right)+\left(xy^\prime+x^\prime y-yy^\prime\right)\omega.\end{alignat*}またそれによって商は\begin{alignat*}{1}\frac{x^\prime+y^\prime\omega}{x+y\omega}&=\frac{\ \left(x^\prime+y^\prime\omega\right)\left(x+y\overline{\omega}\right)\ }{\left(x+y\omega\right)\left(x+y\overline{\omega}\right)}\\[2mm]&=\frac{\ \ \left(x^\prime+y^\prime\omega\right)\left(x-y-y\omega\right)\ \ }{x^2-xy+y^2}\end{alignat*}で $\left(\ 1\ \right)$ のような形の数に等しい.$\left(\ 1\ \right)$ のような数の全部が二次体 $K\left(\sqrt{-3}\right)$ を組成するのである.
この計算で $\omega^2+\omega+1=0$ を用いた.また $x+y\omega$ と共軛な複素数 $x+y\overline{\omega}=\left(x-y\right)-y\omega$ もやはり $\left(\ 1\ \right)$ の形の数であり,かつ $N\left(x+y\omega\right)=\left(x+y\omega\right)\left(x+y\overline{\omega}\right)=x^2-xy+y^2$ は正の有理数である.
$\left(\ 1\ \right)$ のような数の中で $x$,$y$ が有理整数であるものだけを二次体 $K\left(\sqrt{-3}\right)$ の整数ということにする.しからばこのように拡張された意味においても,整数の和,差および積はやはり整数であるが,商は一般には整数でない.本節では,このような整数をギリシャ文字で表わし,有理数はローマ字で表わすことにする.
整数といっても,$\S\S\ 36\sim38$ で取り扱った Gauss の複素整数 $a+bi$ とは全く別のものである($x+y\omega$ を $a+bi$ の形に書けば,$a=x-\left(y/2\right)$,$b=y\sqrt{3}/2$ で,$b$ は有理数でない).
このように整数の意味を規定して,それに基づいて整数,倍数,約数,それからまた単数,同伴数などを $\S\ 36$ と同様に定義することができる.ただし概念の構成は同様でも,結果はもちろん違う.まず単数 $\varepsilon=x+y\omega$ は $N\left(x+y\omega\right)=1$ なる整数である.故に\[x^2-xy+y^2=1,\]すなわち\[\left(2x-y\right)^2+3y^2=4.\] よって $y=0$ したがって $x=\pm1$.あるいは $y^2=1$ したがって $x\left(x\mp1\right)=0$ すなわち,$x=0$,$y=\pm1$,または $x=\pm1$,$y=\pm1$.故に単数は $\pm1$ のほか,\[\pm\omega,\hphantom{\omega}\pm\left(1+\omega\right)=\mp\omega^2.\]すなわち合わせて六つある.それらはすなわち $1$ の六乗根である.
最も重要なのは除法に関する基本定理である.
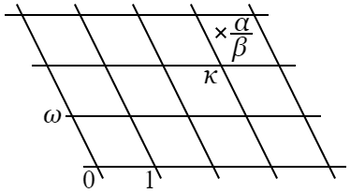
$\alpha$ と $\beta$($\neq0$)とが与えられた整数であるとき,\[\alpha=\beta\kappa+\rho,\hphantom{\rho}\left|\rho\right|\lt\left|\beta\right|\]になるような整数 $\kappa$,$\rho$ が存在する.
ここでは,整数を複素数平面上の点で表わすとき,それは $120^\circ$ の角を有する菱形を基本とする格子の点である.
 |
長くなるから,以下要点だけを説明することにするけれども,読者が練習問題として $\S\ 36$ にならって綿密に考察することを望むのである.
$\boldsymbol{2.}$ 二次体 $K\left(\sqrt{-3}\right)$ における素数 $\pi$ は有理素数 $p$ の約数である.したがって $N\pi=p$ または $N\pi=p^2$.
さて $N\pi=p^2$,$\pi\overline{\pi}=p^2$ なるときは,素因数分解の一意性によって $\pi$ は $p$ の同伴数である.すなわち有理素数がそのまま $K\left(\sqrt{-3}\right)$ における素数である.
また $N\pi=p$,すなわち $p=\pi\overline{\pi}$ で,有理素数 $p$ が二つの素因数に分解されるときには,\[\pi=x-y\omega\]とおけば\[x^2+xy+y^2=p.\tag{$\ 2\ $}\] ここでは $p=3$ が重大である.恒等式\[x^2+x+1=\left(x-\omega\right)\left(x-\overline{\omega}\right)\]において,$x=1$ とおけば,\[3=\left(1-\omega\right)\left(1-\overline{\omega}\right)\]よって $1-\omega$ が一つの素数であるが,\[1-\overline{\omega}=1-\omega^2=\left(1+\omega\right)\left(1-\omega\right)=-\omega^2\left(1-\omega\right)\]であるから,\[3=-\omega^2\left(1-\omega\right)^2.\] 本節では $\lambda=1-\omega$ とする.しからば $3$ は $\lambda^2$ の同伴数である.すなわち素因数分解の意味において(単数因子を無視すれば),$3$ が素数 $\lambda$ の平方である.
〔注意〕 ここの $\lambda=1-\omega$ は $\S\ 36$ の $\lambda=1-i$ に類似する特別な素数である.\[\lambda=1-\frac{-1+\sqrt{-3\vphantom{1^1}}}{2}=\frac{3-\sqrt{-3\vphantom{1^1}}}{2}=\sqrt{-3\vphantom{1^1}}\times\frac{-1-\sqrt{-3\vphantom{1^1}}}{2}=\overline{\omega}\sqrt{-3\vphantom{1^1}}.\] すなわち $\lambda=1-\omega$ は $\sqrt{-3\vphantom{1^1}}$ の同伴数である.
〔問題 $\boldsymbol{1}$〕 $K\left(\sqrt{-3}\right)$ の整数 $\xi=x-y\omega$ が $\lambda$(すなわち $\sqrt{-3}$)で割り切れるのは $x\equiv y\hphantom{3}\left(\text{mod}.\ 3\right)$ であるときである.
〔解〕 $\lambda=1-\omega$.$\therefore\hphantom{1}\omega=1-\lambda\hphantom{1}\therefore\hphantom{1}x-y\omega=x-y+y\lambda$.これが $\lambda$ で割れるのは,有理整数 $x-y$ が $\lambda$ で,したがって $3$ で割れるときに限る.
〔注意〕 $\xi$ が $\lambda$ で割れないならば,$x-y\equiv\pm1\left(\text{mod}.\ 3\right)$,故に $\xi=\pm1+\lambda\eta$,ただし,$\eta$ は $K\left(\sqrt{-3}\right)$ の整数である.あるいは $\xi=\pm1+\eta\sqrt{-3}$ と書いてもよい.
次に $p\neq3$ なるとき,$\left(\ 2\ \right)$ に解があるとして,\[\pi=a-b\omega すなわち p=a^2+ab+b^2\]と置けば,\[4p=\left(2a+b\right)^2+3b^2.\]故に\[\left(\frac{4p}{3}\right)=1,\]したがって\[\left(\frac{p}{3}\right)=1.\]故に($\S\ 12$)\[p\equiv1\hphantom{3}\left(\text{mod}.\ 3\right).\tag{$\ 3\ $}\]これが $\left(\ 2\ \right)$ に解があるために必要な条件であるが,それはまた十分な条件である.この条件のもとにおいて\[\left(\frac{-3}{p}\right)=1\](平方剰余の相互法則.$\S\ 13$ 参照).故に\[r^2\equiv-3\hphantom{m}\left(\text{mod}.\ p\right)\tag{$\ 4\ $}\]なる有理整数 $r$ が存在する.よって\[\left(p,\hphantom{r}r-\sqrt{-3}\right)=\delta\]と置けば,$\delta=1$,あるいは $\delta=p$,あるいはまた $\delta=\pi$,$p=\pi\overline{\pi}$ でなければならない.$\delta=1$ とすれば,共軛数に関しても,$\left(p,\ r+\sqrt{-3}\right)=1$,したがって $\left(r-\sqrt{-3}\right)\left(r+\sqrt{-3}\right)=r^2+3$ が $p$ と互いに素で $\left(\ 4\ \right)$ に矛盾する.また $r-\sqrt{-3}=\left(r-1\right)-2\omega$ は $p$ で割り切れないから,$\delta=p$ も不可能である.故に $\delta=\pi$,$p=\pi\overline{\pi}$ である.
$\left(r-1\right)-2\omega$ が $p$ で割り切れるならば,$p=2$.それは $\left(\ 3\ \right)$ に合わない.
さて $\pi=\left(p,\ r-\sqrt{-3}\right)$,$\overline{\pi}=\left(p,\ r+\sqrt{-3}\right)$,したがって\[\left(\pi,\ \overline{\pi}\right)=\left(p,\ r-\sqrt{-3},\ r+\sqrt{-3}\right)\]であるが,$\left(r-\sqrt{-3}\right)+\left(r+\sqrt{-3}\right)=2r$ は,$\left(\ 4\ \right)$ から見えるように,$p$ で割り切れない($p\neq3$).故に,\[\left(\pi,\ \overline{\pi}\right)=1,\]したがって $\pi$ と $\overline{\pi}$ とは同伴数ではあり得ない.
以上要約すれば:
二次体 $K\left(\sqrt{-3}\right)$ において $3$ は素数 $\sqrt{-3}$ の平方(と同伴)である.
$p\equiv1\hphantom{3}\left(\text{mod}.\ 3\right)$ なる有理素数 $p$ は二つの相異なる(同伴でない)素因数に分解される.
$p\equiv2\hphantom{3}\left(\text{mod}.\ 3\right)$ なる有理素数 $p$ は分解されない.すなわち $K\left(\sqrt{-3}\right)$ においても素数である.
さて $p\equiv1\hphantom{m}\left(\text{mod}.\ 3\right)$\[p=\pi\overline{\pi},\hphantom{\pi}\pi=a-b\omega,\hphantom{\pi}4p=\left(2a+b\right)^2+3b^2\tag{$\ 5\ $}\]において $\pi$ をその同伴数なる $\pm\pi$ または\begin{alignat*}{1}\pm\omega\pi&=\pm\left\{b+\left(a+b\right)\omega\right\},\\[2mm]\pm\omega^2\pi&=\mp\left\{\left(a+b\right)+a\omega\right\}\end{alignat*}で置き換えることができる.しかるに,$a$,$b$ がともに偶数であることはできないから,$b$,$a+b$,$a$ のうち一つだけが偶数である.よって初めから $\pi=a-b\omega$ において,$b$ は偶数であるとしてもよい.しからば $\left(\ 5\ \right)$ の両辺を $4$ で割って\[p=x^2+3y^2\]を得る.よって有理整数に関する次の定理を得る.
〔定理 $\boldsymbol{4.\ 4}$〕 有理素数 $p$ に関して,$p=x^2+3y^2$ が整数解を有するために必要かつ十分な条件は $p=3$ または $p\equiv1\left(\text{mod}.\ 3\right)$ である.正の整数解はただ一組に限る.
$p=3$ の場合には $x=0$,$y=1$.
〔例〕 $7=2^2+3\hspace{0.7mm}\cdotp1^2$,$13=1^2+3\hspace{0.7mm}\cdotp2^2$,$19=4^2+3\hspace{0.7mm}\cdotp1^2$.等々.
| 〔問題 $\boldsymbol{2}$〕 | $a=x^2+3y^2$, $\left(x,\ y\right)=1$ |
〔解〕 定理 $4.\ 3$ と同様.
| 〔例〕 | $\begin{alignat*}{1}7&=N\left(2+\sqrt{-3\vphantom{3^n}}\right).\hphantom{1}13=N\left(1+2\sqrt{-3\vphantom{3^n}}\right).\\[2mm]91&=N\left(2+\sqrt{-3\vphantom{3^n}}\right)\left(1+2\sqrt{-3\vphantom{3^n}}\right)=N\left(-4+5\sqrt{-3\vphantom{3^n}}\right)=4^2+3\hspace{0.7mm}\cdotp5^2\\[2mm]&=N\left(2+\sqrt{-3\vphantom{3^n}}\right)\left(1-2\sqrt{-3\vphantom{3^n}}\right)=N\left(8-3\vphantom{3^n}\sqrt{-3\vphantom{3^n}}\right)=8^2+3\hspace{0.7mm}\cdotp3^2.\end{alignat*}$ |