附 録
$\S\ 58.$ イデヤルの類の数 $\boldsymbol{h}$ の計算
$\boldsymbol{1.}$ 十九世紀の初頭において Gauss の「整数論」(Disquisitiones arithmeticae,$1801$)は時代を超越することあまりにはなはだしくて,学界の無理解の中に埋没せんとする危険なる状態にあったのであろう.現に $1830$ 年に至って出た Legendre の Théorie des nombres 第四版は(書名からは勇敢に Essai の語を削ったけれども)依然として雑纂的の旧態を改めていない.越えて $1832$ 年にはすでに Gauss の複素整数論が出ている.ハンディキャップはあまりに大きいのである.このような時世において,Gauss の整数論の平易化と普及とに努力して倦むことを知らなかったのは Dirichlet である.彼が旅中にもすりきれた Disquisitiones 一部を必ず行李の中に収めて寸時も身を離さなかったことは有名なる逸話である.
その Dirichlet は整数論において Gauss 以外別に一生面を開拓した.Dirichlet の名著「整数論への微積分法の種々の応用」(Recherches sur diverses applications de l'analyse infinitésimale à la théorie des nombres,Crelle 誌 $19$ 巻,$1840$)は画時代的で,それが端緒となって,現今の解析的整数論が発育したのである.Dirichlet が取り扱った問題の中で最も重要なのは,二次体におけるイデヤルの類の数 $h$ の計算(現代化していう)と算術級数中の素数の問題($21$ 頁)とである.いまここでその概略を紹介する.
Dirichlet が得た $h$ の公式は後に述べるが,それに到達するまでの行程は随分長いから,証明の末節にとらわれていては,要点を補捉することが困難であろうと思われる.よって本節では証明の細目,特に函数論的の側面(収束の問題など)はなるべく節略して,Dirichlet の着想の要所を主眼として述べる.
$\boldsymbol{2.}$ 〔定理 $\boldsymbol{6.\ 10}$〕 二次体 $K\left(\sqrt{m}\right)$ において,各類に属するイデヤル $J$ の中で,$\mathrm{N}\left(J\right)\leqq t$ であるものの数を $T_0\left(t\right)$ とすれば,\[\underset{t\rightarrow\infty}{\operatorname{Lim}}\frac{T_0}{t}=\kappa.\] ここで $\kappa$ の値は類を狭義($\S\ 54$ 参照)にとるならば次の通りである.\begin{alignat*}{1}&m\lt0:\hspace{2cm}\kappa=\frac{\pi}{w\sqrt{\left|d\right|}},\tag{$\ 1\ $}\\[2mm]&m\gt0:\hspace{2cm}\kappa=\frac{\log\varepsilon}{\sqrt{d}}.\tag{$\ 2\ $}\end{alignat*}ただし,$d$ は二次体 $K\left(\sqrt{m}\right)$ の判別式で,$\left(\ 1\ \right)$ においては,$2w$ が単数の数(すなわち一般には $w=1$,$K\left(i\right)$ では $w=2$,$K\left(\sqrt{-3}\right)$ では $w=3$).また $\left(2\right)$ では $\varepsilon$ は $t^2-du^2=4$ の最小正数解に対応する単数である($N\left(\varepsilon\right)=1$).簡明にいえば,二次体の各類において,ノルムの大きさに関してのイデヤルの密度 $\boldsymbol{\left(\kappa\right)}$ は共通の有限値を有する.
〔注意〕 $\left(\ 1\ \right)$ において $w$ を上記のような意味で付けて置けば,これから述べる方法は一般に($m=-1$,$-3$ の場合にも)通用するが,この二つの特別の場合には $h=1$ であるから,簡単のためにそれを除くことにする.すなわち $\left(\ 1\ \right)$ の代わりに\[m\lt0,\hphantom{m}m\neq-1,\hphantom{m}m\neq-3:\hspace{1cm}\kappa=\frac{\pi}{\sqrt{\left|d\right|}}\tag{$\ 1^{\large*}$}\]をとる.
〔証〕 与えられた類に属するイデヤルを一般的に $J$ で表わし,その逆の類から一つのイデヤル $A$ を取れば,$AJ=\left(\alpha\right)$ は主類(狭義)に属する,すなわち $N\left(\alpha\right)\gt0$.
逆に $\alpha$ を $A$ に含まれる $N\left(\alpha\right)\gt0$ なる整数とすれば,$\left(\alpha\right)=AJ$ で,$J$ は与えられた類に属する.故に $T_0$ はイデヤル $A$ に含まれる整数 $\alpha$ の中で,\[0\lt N\left(\alpha\right)\leqq \mathrm{N}\left(A\right)t\]なる条件に適合して,かつ互いに同伴数でないものの数である.
まず虚の二次体を考察する.この場合 $A$ を原始イデヤルとして $\left[a,\ \theta\right]$($\theta=r+\omega$)をその標準的底とする.しからば\[\alpha=ax+\theta y,\hphantom{1}0\lt N\left(\alpha\right)\leqq at\tag{$\ 3\ $}\]で,$\alpha$ と $-\alpha$ とだけが同伴である(上記注意,参照)から $\left(\ 3\ \right)$ を満足せしめる格子点 $\left(x,\ y\right)$ の数が $2T_0$ である.
さて\[N\left(\alpha\right)=\left(ax+\theta y\right)(ax+\overline{\theta}y)=a(ax^2+bxy+cy^2)\]と置けば\[b^2-4ac=d.\] 二次方程式 $ax^2+bx+c=0$ の根が $-\theta/a$,$-\overline{\theta}/a$ で,$\theta-\overline{\theta}=\omega-\overline{\omega}=i\sqrt{\left|d\right|}$ だから $(\theta-\overline{\theta}{}^2)=b^2-4ac=d$.
$\left(\ 3\ \right)$ の条件は\[ax^2+bxy+cy^2\leqq t\]
 |
ここでは $N\left(\alpha\right)\gt0$ であるから,$\varepsilon$ は $N\left(\varepsilon\right)=1$ なる基本単数($N\left(\varepsilon\right)=1$,$\varepsilon\gt1$ なる $\varepsilon$ の中の最小のもの)としてよろしい.
さて $\pm\alpha\varepsilon^n$ において $\pm$ を適当にとって初めから $\alpha\gt0$,$\alpha^\prime\gt0$ として,\[\alpha_0=\alpha\varepsilon^n,\hspace{1cm}\alpha_0{}^\prime=\alpha^\prime\varepsilon^{\prime\ \!n}=\frac{\alpha^\prime}{\varepsilon^n}\]と置けば\[\frac{\alpha_0{}^\prime}{\alpha_0}=\frac{\alpha^\prime}{\alpha}\varepsilon^{-2n}.\]故に $n$ を適当にとれば\[1\leqq\frac{\alpha_0{}^\prime}{\alpha_0}\lt\varepsilon^2\]ならしめることができる.$\alpha$ の同伴数の中に,この条件に適合する $\alpha_o$ が一つ,しかもただ一つあって,われわれの問題においては,このような分離条件に適合する $\alpha$ だけを数えればよいのである.
すなわち前と同じ記号を用いるならば,$T_0$ は\[\alpha=ax+\theta y,\hphantom{1}0\lt N\left(\alpha\right)\leqq at,\\[2mm]\alpha\gt0,\hspace{5mm}1\leqq\frac{\alpha^\prime}{\alpha}\lt\varepsilon^2\]なる整数格子点 $\left(x,\ y\right)$ の数である.あるいは前のように $1/\sqrt{\ t\ }$ に縮小すれば,$\operatorname{Lim}\ \!\!\!T_0/t$ は\begin{eqnarray*}0\lt ax^2+bxy+cy^2&\leqq&1,\\[2mm]1\leqq\frac{ax+\theta^\prime y}{ax+\theta y}&\lt&\varepsilon^2,\\[2mm]ax+\theta y&\gt&0\end{eqnarray*}なる範囲(それは双曲線の弧と中心からその両端に至る二つの動径とで囲まれた扇形)の面積である.
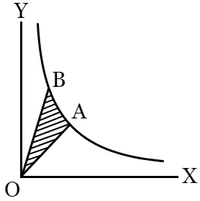 |
$\boldsymbol{3.}$ いま $T$ を二次体における $\mathrm{N}\left(J\right)\leqq t$ なるなるイデヤル $J$ の総数とし,$h$ をイデヤルの類の数(狭義)とすれば,上記定理によって\[\underset{t\rightarrow\infty}{\operatorname{Lim}}\frac{T}{t}=h\kappa.\tag{$\ 4\ $}\] $\kappa$ は既知であるから,$h$ を求めることは $\left(\ 4\ \right)$ の左辺の極限値を求めることに帰する.
Dirichlet のこの着意に基づいて $\operatorname{Lim}\ \!\!\!\left(T/t\right)$ を求める近代的の工夫もあるが,ここでは Dirichlet の原証明をイデヤル論に順応せしめてその概略を紹介する.
$\boldsymbol{4.}$ Dirichlet の方法によれば,次の三つの無限級数を考察する必要がある.
その第一は古典的な級数\[\zeta\left(s\right)=\overset{\infty}{\underset{n=1}{\textstyle\sum}}\frac{1}{\ n^s\ }\hspace{2cm}\left(s\gt1\right)\]である.この級数は $s\gt1$ なるとき収束することはよく知られているが,後に Riemann がそれを複素変数 $s$ の函数として素数の数 $\pi\left(x\right)$($22$ 頁)を求める問題に応用したから,現今それを Riemann の $\boldsymbol{\zeta}$ 函数といっている.
上記 $\zeta\left(s\right)$ を次のように無限積に展開することができる:\[\zeta\left(s\right)=\overset{p}{\textstyle\prod}\frac{1}{\ 1-p^{-s}\ },\hphantom{s}\left(s\gt1\right)\]積はすべての有理素数 $p$ の上にわたるのである.
正の整数 $n$ が一意的に素数巾の積に分解されるから\begin{alignat*}{1}\overset{p}{\textstyle\prod}&\frac{1}{\ 1-p^{-s}\ }=\overset{p}{\textstyle\prod}\left(1+\frac{\ 1\ }{p^s}+\frac{\ 1\ }{p^{2s}}+\cdots\cdots\right)\\[2mm]&=\left(1+\frac{\ 1\ }{2^s}+\frac{\ 1\ }{2^{2s}}+\cdots\cdots\right)\left(1+\frac{\ 1\ }{3^s}+\frac{\ 1\ }{3^{2s}}+\cdots\cdots\right)\cdots\cdots\left(1+\frac{\ 1\ }{p^s}+\frac{\ 1\ }{p^{2s}}+\cdots\cdots\right)\cdots\\[2mm]&\ =\overset{\left(\alpha,\ \beta,\cdots,\ \lambda\ ,\cdots\right)}{\textstyle\sum}\frac{1}{\left(2^\alpha3^\beta\cdots p^\lambda\cdots\right)^s}=\overset{\infty}{\underset{n=1}{\textstyle\sum}}\frac{\ 1\ }{n^s}.\end{alignat*}$s\gt1$ ならば,収束の問題は明白である.
第二は二次体 $K\left(\sqrt{m}\right)$ のすべてのイデヤル $J$ の上にわたる級数\[\zeta_K\left(s\right)=\overset{J}{\textstyle\sum}\frac{1}{\mathrm{N}\left(J\right)^s}\]である.Dedekind が任意の代数体 $K$ に関してこのような級数を $s$ の函数として考察したから,いまはそれを数体 $K$ に関する Dedekind の $\boldsymbol{\zeta}$ 函数という.
この級数も $s\gt1$ なるときに収束するが,いま $\mathrm{N}\left(J\right)=n$ なるイデヤル $J$ の数を $F\left(n\right)$ で表わすならば\[\zeta_K\left(s\right)=\overset{\infty}{\underset{n=1}{\textstyle\sum}}\frac{\ \!F\left(n\right)\ }{n^s}.\]イデヤル $J$ が一意的に素因子に分解されることから,$\zeta_K\left(s\right)$ を無限積に展開することができる.Riemann の $\zeta\left(s\right)$ と同様である.すなわち\[\zeta_K\left(s\right)=\overset{P}{\textstyle\prod}\frac{1}{\ \!1-\mathrm{N}\left(P\right)^{-s}},\]ここでは積は二次体 $K\left(\sqrt{m}\right)$ におけるすべての素なイデヤル $P$ の上にわたるのである.
二次体における素のイデヤルの三種の区別にしたがって\begin{alignat*}{2}p&={PP}^\prime\hspace{1cm}\left(P\neq P^\prime\right),&\hspace{1cm}\mathrm{N}\left(P\right)&=p,\\[2mm]q&=Q,&\mathrm{N}\left(Q\right)&=q^2,\\[2mm]l&=L^2,&\mathrm{N}\left(L\right)&=l\end{alignat*}と置けば,上記の無限積を次のように表わすことができる:\begin{alignat*}{1}\zeta_K\left(s\right)&=\overset{l}{\textstyle\prod}\frac{1}{1-l^{-s}}\hspace{0.7mm}\cdotp\left(\overset{p}{\textstyle\prod}\frac{1}{1-p^{-s}}\right)^2\cdotp\hspace{0.7mm}\overset{q}{\textstyle\prod}\frac{1}{1-q^{-2s}}\\[2mm]&=\left(\overset{l}{\textstyle\prod}\frac{1}{1-l^{-s}}\overset{P}{\textstyle\prod}\frac{1}{1-p^{-s}}\overset{q}{\textstyle\prod}\frac{1}{1-q^{-s}}\right)\left(\overset{p}{\textstyle\prod}\frac{1}{1-p^{-s}}\overset{q}{\textstyle\prod}\frac{1}{1+q^{-s}}\right).\end{alignat*}ここで第一の括弧内の積は Riemann の $\zeta\left(s\right)$ である.また第二の括弧内の積は,$\chi\left(l\right)=0$,$\chi\left(p\right)=1$,$\chi\left(q\right)=-1$ を用いて($295$ 頁)$p$,$q$,$l$ を統一的に $p$ で表わせば\[L_K\left(s\right)=\overset{p}{\textstyle\prod}\frac{1}{1-\chi\left(p\right)p^{-s}}\]になる.この無限積は $\chi\left(mn\right)=\chi\left(m\right)\chi\left(n\right)$ を用いて,次のように無限級数に変形される($\zeta\left(s\right)$,$\zeta_K\left(s\right)$ と同様):\[L_K\left(s\right)=\overset{\infty}{\underset{n=1}{\textstyle\sum}}\frac{\chi\left(n\right)}{n^s}.\tag{$\ 5\ $}\]故に\[\zeta_K\left(s\right)=\zeta\left(s\right)L_K\left(s\right).\]この「$L$ 函数」 $L_K\left(s\right)$ が考察を要する第三の級数である.
$\boldsymbol{5.}$ 上記の無限級数も無限積も $s\gt1$ なるとき絶対収束をすることは容易にわかる.上文に述べた等式は $s\gt1$ なる仮定のもとにおいて成り立つものである.
Dirichlet の方法では,$s\rightarrow1$ のときにおける上記三つの函数 $\zeta\left(s\right)$,$\zeta_K\left(s\right)$,$L_K\left(s\right)$ の性状が基本的である.すなわち
$\left[\ 1\ \right]$ $\underset{s\rightarrow1}{\operatorname{Lim}}\left(s-1\right)\zeta\left(s\right)=1$.
$\left[\ 2\ \right]$ $\underset{s\rightarrow1}{\operatorname{Lim}}\left(s-1\right)\zeta_K\left(s\right)=h\kappa$.
$\left[\ 3\ \right]$ $L_K\left(s\right)$ は $s\gt0$ なるとき収束する.しかも $s\gt s_0$($\gt0$)なる範囲において一様に収束する.故に $L_K\left(s\right)$ は $s=1$ において連続的である.したがって\[\underset{s\rightarrow1}{\operatorname{Lim}}L_K\left(s\right)=L_K\left(\ 1\ \right)=\overset{\infty}{\underset{n=1}{\textstyle\sum}}\frac{\chi\left(n\right)}{n}.\] これらが承認されるならば,$\left(\ 4\ \right)$,$\left(\ 5\ \right)$,$\left[\ 1\ \right]$,$\left[\ 2\ \right]$ から\[h\kappa=\overset{\infty}{\underset{n=1}{\textstyle\sum}}\frac{\chi\left(n\right)}{n}.\tag{$\ 6\ $}\]よって $h$ が無限級数の和として求められることになって,$h$ の計算がここで一段落をなすのである.
〔証 $\boldsymbol{1}$〕\[\int_n^{n+1}\frac{dx}{x^s}\lt\frac{1}{n^s}\lt\int_{n-1}^n\frac{dx}{x^s}\hspace{1cm}\left(n\gt1,\hphantom{m}s\gt1\right)\]から\[\int_1^\infty\frac{dx}{x^s}\lt\zeta\left(s\right)\lt1+\int_1^\infty\frac{dx}{x^s},\]
| すなわち | $1\lt\left(s-1\right)\zeta\left(s\right)\lt s,$ |
簡明のために $\chi\left(n\right)=c_n$ とおく.しからば $\displaystyle\overset{\left|\ d\ \right|}{\underset{n=1}{\textstyle\sum}}\chi\left(n\right)=0$($122$ 頁参照)だから,\[S\left(n\right)=c_1+c_2+\cdots\cdots+c_n\]とおけば,任意の $n$ に関して $\left|S\left(n\right)\right|\lt C$ なる一定の $C$ がある(例えば $C=\varphi\left(\ \!\!\left|d\right|\ \!\!\right)$ でよい).故に\begin{alignat*}{1}\overset{\mu}{\underset{n=\nu}{\textstyle\sum}}\frac{c_n}{n^s}&=\overset{\mu}{\underset{n=\nu}{\textstyle\sum}}\frac{S\left(n\right)-S\left(n-1\right)}{n^s}\\[2mm]&=\frac{S\left(\mu\right)}{\mu^s}-\frac{S\left(\nu-1\right)}{\nu^s}+\overset{\mu-1}{\underset{n=\nu}{\textstyle\sum}}S\left(n\right)\left(\frac{1}{n^s}-\frac{1}{\left(n+1\right)^s}\right).\end{alignat*}よって,$s\gt0$ なるとき(特に $s\gt s_0$ なる範囲において)\begin{alignat*}{1}\left|\overset{\mu}{\underset{n=\nu}{\textstyle\sum}}\frac{c_n}{n^s}\right|&\lt\frac{C}{\mu^s}+\frac{C}{\nu^s}+C\overset{\mu-1}{\underset{n=\nu}{\textstyle\sum}}\left(\frac{1}{n^s}-\frac{1}{\left(n+1\right)^s}\right)\\[2mm]&\lt\frac{C}{\mu^s}+\frac{C}{\nu^s}+C\left(\frac{1}{\nu^s}-\frac{1}{\mu^s}\right)=\frac{2C}{\nu^s}\lt\frac{2C}{\nu^{s_0}}.\end{alignat*} 〔証 $\boldsymbol{2}$〕 $\zeta_K\left(s\right)=\sum F\left(n\right)/n^s$ において $F\left(n\right)=c_n$,$c_1+c_2+\cdots\cdots+c_n=S\left(n\right)$ とすれば,$S\left(n\right)$ は $t=n$ に対する $T$ であることから,$\left(\ 4\ \right)$ によって\[\underset{n\rightarrow\infty}{\operatorname{Lim}}\frac{S\left(n\right)}{n}=h\kappa.\]いま簡便のために $h\kappa=a$,$\dfrac{S\left(n\right)}{n}=a+o_n$ とおけば,$n\rightarrow\infty$ のとき,\[o_n\rightarrow0.\]故に $s\gt1$ のとき\begin{alignat*}{1}\left|\zeta_K\left(s\right)-a\zeta\left(s\right)\vphantom{\overset{\infty}{\underset{1}{\textstyle\sum}}}\right|&=\left|\overset{\infty}{\underset{n=1}{\textstyle\sum}}\frac{\ no_n-\left(n-1\right)o_{n-1}\ }{n^s}\right|=\left|\overset{\infty}{\underset{n=1}{\textstyle\sum}}no_n\left(\frac{\ 1\ }{n^s}-\frac{1}{\ \left(n+1\right)^s\ }\right)\right|\\[2mm]&=s\left|\overset{\infty}{\underset{n=1}{\textstyle\sum}}no_n\int_n^{n+1}\frac{dx}{x^{s+1}}\right|\lt s\overset{\infty}{\underset{n=1}{\textstyle\sum}}\left|o_n\right|\int_n^{n+1}\frac{\ \!dx\ \!}{x^s}.\end{alignat*}いま任意に与えられた $\delta\gt0$ に対して整数 $N$ を十分大きくとって,$n\gt N$ のとき $\left|o_n\right|\lt\delta$ とし,また $\left|o_n\right|$($n\leqq N$)の上限を $m$ とすれば\[\left|\zeta_K\left(s\right)-a\zeta\left(s\right)\right|\lt ms\int_1^N\frac{dx}{x}+s\delta\int_N^\infty\frac{dx}{x^s}\\[2mm]=ms\log N+\frac{s\delta}{s-1}N^{-s+1},\]故に\[\underset{s\rightarrow1}{\operatorname{Lim}}\left|\left(s-1\right)\zeta_K\left(s\right)-a\left(s-1\right)\zeta\left(s\right)\vphantom{\frac{}{}}\right|\leqq\delta.\]$\delta\gt0$ は任意であるから,この $\operatorname{Lim}$ は $0$ に等しい.故に $\left[\ 1\ \right]$ によって\[\operatorname{Lim}\ \!\!\!\left(s-1\right)\zeta_K\left(s\right)=a=h\kappa.\]以上で $\left[\ 1\ \right]$,$\left[\ 2\ \right]$,$\left[\ 3\ \right]$ の説明を終わる.
Gauss の和は有名である.それは次の通り.\[\overset{r}{\textstyle\sum}\chi\left(r\right)\exp\left(\frac{2\pi i}{\left|d\right|}nr\right)=\chi\left(n\right)\sqrt{d}.\tag{$\ 7\ $}\]和は $\text{mod}.\ d$ に関する(既約)代表の一組 $r$ の上にわたる.$\exp\left(\theta i\right)$ は $e^{\theta i}=\cos\theta+i\sin\theta$ で,ここでは $1$ の原始 $\left|d\right|$ 乗根なる $\rho=\exp\left(2\pi i/\left|d\right|\right)$ の $nr$ 乗が和の一般項に入るのである.すなわち左辺の和は\[\overset{r}{\textstyle\sum}\chi\left(r\right)\rho^{nr},\] 最も大切なのは右辺の $\sqrt{d}$ の意味である.それは $d\gt0$ ならば $\left|\ \!\sqrt{d}\ \right|$,また $d\lt0$ ならば $i\sqrt{\left|d\right|}$ である.$d$ はもちろん二次体 $K\left(\sqrt{m}\right)$ の判別式で,$\chi\left(r\right)$ は Kronecker の記号 $\left(\dfrac{d}{r}\right)$ である.
$\left(\ 7\ \right)$ の証明は簡単でない.それはあとまわしにして($\S\ 60$),ここでは $\left(\ 7\ \right)$ を用いて $h$ の計算を片付ける.
$\left(\ 6\ \right)$,$\left(\ 7\ \right)$ から\begin{alignat*}{1}h\kappa\sqrt{d}&=\overset{\infty}{\underset{n=1}{\textstyle\sum}}\frac{\chi\left(n\right)\sqrt{d}}{n}=\overset{\infty}{\underset{n=1}{\textstyle\sum}}\overset{\left|d\right|}{\underset{r=1}{\textstyle\sum}}\frac{1}{n}\chi\left(r\right)\exp\left(\frac{2\pi i}{\left|d\right|}nr\right)\\[2mm]&=\underset{r}{\textstyle\sum}\chi\left(r\right)\underset{n}{\textstyle\sum}\frac{1}{n}\exp\left(\frac{2\pi i}{\left|d\right|}nr\right).\end{alignat*} 和の順序を換えてもよいのは,
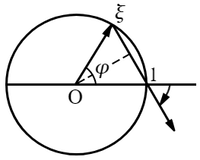 |
$\log$ の意味は一時かりに $\xi=\cos\varphi+i\sin\varphi$ と置けば,\begin{alignat*}{1}\left|1-\xi\right|=2\sin\frac{\varphi}{2},\hspace{5mm}&\operatorname{arc}\left(1-\xi\right)=-\left(\frac{\pi}{2}-\frac{\varphi}{2}\right),\\[2mm]&0\leqq\varphi\leqq2\pi\end{alignat*}\[\log\left(1-\xi\right)=\log\left(2\sin\frac{\varphi}{2}\right)-i\left(\frac{\pi}{2}-\frac{\varphi}{2}\right).\] よって\[h\kappa\sqrt{d}=-\overset{\left|\ d\ \right|}{\underset{r=1}{\textstyle\sum}}\chi\left(r\right)\log\left(1-\xi^r\right).\] これから実数部と虚数部とを分けて,また $\underset{r}{\sum}\chi\left(r\right)=0$ に注意して,$d\gt0$ のとき,\begin{alignat*}{1}h\kappa\sqrt{d}&=-\underset{r}{\textstyle\sum}\chi\left(r\right)\log\left(2\sin\frac{\pi r}{d}\right)\\[2mm]&=-\underset{r}{\textstyle\sum}\chi\left(r\right)\log\sin\frac{\pi r}{d}.\end{alignat*}$d\lt0$ のとき,\begin{alignat*}{1}h\kappa\textstyle\sqrt{\ \!\left|d\right|\ \!}&=\underset{r}{\textstyle\sum}\chi\left(r\right)\left(\frac{\pi}{2}-\frac{\pi r}{\left|d\right|}\right)\\[2mm]&=-\frac{\pi}{\left|d\right|}\overset{\left|\ d\ \right|}{\underset{r=1}{\textstyle\sum}}\chi\left(r\right)r.\end{alignat*} よって $\kappa$ の値($372$ 頁 $\left(\ 1\ \right)$,$\left(\ 2\ \right)$)を入れ,$0\lt r\lt\left|d\right|$ なる $r$ を\[\chi\left(r\right)=1 または \chi\left(r\right)=-1\]に従ってそれぞれ $a$ または $b$ と記して次の結果を得る.
〔定理 $\boldsymbol{6.\ 11}$〕 (Dirichlet の公式)
| $\begin{alignat*}{1}d&\gt0:\vphantom{\dfrac{\overset{b}{\prod}\dfrac{b}{d}}{\overset{a}{\prod}\dfrac{a}{d}}}\\[2mm]d&\lt0:\vphantom{\dfrac{1}{|}}\end{alignat*}$ | $\left.\begin{alignat*}{1}\varepsilon^h&=\dfrac{\displaystyle\overset{b}{\textstyle\prod}\sin\dfrac{b\pi}{d}}{\displaystyle\overset{a}{\textstyle\prod}\sin\dfrac{a\pi}{d}}\raise{1mm}.\\[2mm]h&=\dfrac{1}{\left|d\right|}\left(\textstyle\sum b-\textstyle\sum a\right).\end{alignat*}\right\}$ |
一方において,$d\gt0$ から,\[\chi\left(d-r\right)=\chi\left(-r\right)=\chi\left(-1\right)\chi\left(r\right)=\chi\left(r\right).\hphantom{m}\left(\cssId{eq1}{298\ 頁}\right)\] 故に $0\lt r\lt d/2$ なる区間に属する $a$,$b$ と同時に $d/2\lt r\lt d$ に属する $d-a$,$d-b$ がやはりそれぞれ $a$,$b$ の中にあるから,右辺は\[\left({\textstyle\prod}^{\ \prime}\frac{\sin\dfrac{b\pi}{d}}{\sin\dfrac{a\pi}{d}}\right)^2\]に等しい.${\prod}^{\ \prime}$ は $0$ と $d/2$ との間の $a$,$b$ にわたる積である.
よって括弧の中を $E$ とすれば($E\gt0$)\[\varepsilon_0{}^{h_0}=E.\] $E$ は $1$ の $2d$ 乗根の虚数部から組み立てられている.それが二次体 $K\left(\sqrt{d}\right)$ に属する単数であることは,円周等分論からも知られるが,上記の公式において,それが指数 $h_0$ によって基本単数 $\varepsilon_0$ と結び付けられることは,著しい事実というべきであろう.それが何故にそうであるかを,直接に整数論的の手段によって説明することは,現今未開の秘密である.
〔注意 $2$〕 $d\lt0$ の場合には上記の公式をさらに簡約することができる.
まず $d\equiv1\hphantom{4}\left(\text{mod}.\ 4\right)$ のとき,$\chi\left(\left|d\right|-r\right)=\chi\left(-r\right)=-\chi\left(r\right)$ によって\begin{alignat*}{1}\overset{\left|\ d\ \right|}{\underset{r=1}{\textstyle\sum}}\chi\left(r\right)r&={\textstyle\sum}^\prime\chi\left(r\right)r+{\textstyle\sum}^\prime\chi\left(\left|d\right|-r\right)\left(\left|d\right|-r\right)\\[2mm]&=2{\textstyle\sum}^\prime\chi\left(r\right)r-\left|d\right|{\textstyle\sum}^\prime\chi\left(r\right).\end{alignat*}${\sum}^\prime$ は $0$ と $\left|d\right|/2$ との間の $r$ の上にわたる.同じように\begin{alignat*}{1}\overset{\left|\ d\ \right|}{\underset{r=1}{\textstyle\sum}}\chi\left(r\right)r&={\textstyle\sum}^\prime\chi\left(2r\right)2r+{\textstyle\sum}^\prime\chi\left(\left|d\right|-2r\right)\left(\left|d\right|-2r\right)\\[2mm]&=4{\textstyle\sum}^\prime\chi\left(2r\right)r-\left|d\right|{\textstyle\sum}^\prime\chi\left(2r\right)\\[2mm]&=4\chi\left(2\right){\textstyle\sum}^\prime\chi\left(r\right)r-\left|d\right|\chi\left(2\right){\textstyle\sum}^\prime\chi\left(r\right).\end{alignat*}これらの等式に $2$ と $\chi\left(\ 2\ \right)$ とを掛けて引けば\[\left(2-\chi\left(2\right)\ \!\!\right)\overset{\left|\ d\ \right|}{\underset{r=1}{\textstyle\sum}}\chi\left(r\right)r=-\left|d\right|{\textstyle\sum}^\prime\chi\left(r\right).\]よって\[h=\frac{1}{2-\chi\left(2\right)}{\textstyle\sum}^\prime\left(r\right).\tag{$\ 8\ $}\] $d\equiv1$,$5\hphantom{8}\left(\text{mod}.\ 8\right)$ に従って $\chi\left(2\right)=+1$,$-1$ だから\begin{alignat*}{1}d&\equiv1\hphantom{m}\left(\text{mod}.\ 8\right)\ のとき, h={\textstyle\sum}^\prime\chi\left(r\right),\\[2mm]d&\equiv5\hphantom{m}\left(\text{mod}.\ 8\right)\ のとき, h=\frac{1}{3}{\textstyle\sum}^\prime\chi\left(r\right).\end{alignat*} なお,証明は略すが,\[d\equiv0\hphantom{m}\left(\text{mod}.\ 4\right)\\ のとき, h=\frac{1}{2}{\textstyle\sum}^\prime\chi\left(r\right).\]このとき $\chi\left(\ 2\ \right)=0$ であるから,$\left(\ 8\ \right)$ は($d=-3$ と $d=-4$ とを除けば)一般に成立する(補遺 $11$ 参照).
特に $d=-p$ が素数のときには $\chi\left(r\right)=\left(\dfrac{r}{p}\right)$.よって\begin{alignat*}{1}p&\equiv-1\hphantom{n}\left(\text{mod}.\ 8\right)\ ならば, h=\overset{r}{\textstyle\sum}{}^\prime\left(\frac{r}{p}\right).\\[2mm]p&\equiv3\hphantom{m}\left(\text{mod}.\ 8\right)\ ならば, h=\frac{1}{3}\overset{r}{\textstyle\sum}{}^\prime\left(\frac{r}{p}\right).\end{alignat*} この和 ${\sum}^\prime$ は $0$ と $p/2$ との間にある平方剰余と非剰余との数の差である.$h$ はもちろん正の整数であるから,$p\equiv-1\hphantom{4}\left(\text{mod}.\ 4\right)$ のときには,$0$ と $p/2$ との間では平方剰余が非剰余よりも多く,かつ $p\equiv3\hphantom{8}\left(\text{mod}.\ 8\right)$ のときには,この超過が $3$ の倍数である.
この著しい事実を直接に($h$ の計算を迂回しないで)証明することは困難で,今日でも解かれない謎である.
$p\equiv1\ \left(\text{mod}.\ 4\right)$ の場合には,$\left(\dfrac{-1}{p}\right)=1$ だから $\left(\dfrac{r}{p}\right)=\left(\dfrac{p-r}{p}\right)$.したがって $0$ と $p/2$ との間にも,$p/2$ と $p$ との間にも,平方剰余と非剰余とは同数 $\left(p-1\right)/4$ ずつあること明白である.
〔例〕 $p=19$.
| 平 | 方 | 剰 | 余 | $1$,$4$,$5$,$6$,$7$,$9$. | |
| 非 | 剰 | 余 | $2$,$3$,$8$. | ||
まず $s\gt1$ で,$s\rightarrow1$ のとき\[\left(s-1\right)\zeta\left(s\right)\rightarrow1\]から\[\log\left(s-1\right)+\log\zeta\left(s\right)\rightarrow0.\tag{$\ 9\ $}\] さて\begin{alignat*}{1}\log\zeta\left(s\right)&=\log\overset{p}{\textstyle\prod}\frac{1}{1-\dfrac{1}{p^s}}\\[2mm]&=\overset{p}{\textstyle\sum}-\log\left(1-\frac{1}{p^s}\right)\\[2mm]&=\overset{n}{\textstyle\sum}\frac{1}{p^s}+\frac{1}{2}\overset{p}{\textstyle\sum}\frac{1}{p^{2s}}+\frac{1}{3}\overset{p}{\textstyle\sum}\frac{1}{p^{3s}}+\cdots\cdots\end{alignat*} これらの和 $\displaystyle\overset{p}{\textstyle\sum}$ はすべての素数 $p$ の上にわたるのであるが,第二以下の $\sum$ の総和は $s\rightarrow1$ のとき有限である.実際\[\frac{1}{2}\overset{p}{\textstyle\sum}\frac{1}{p^{2s}}+\frac{1}{3}\overset{p}{\textstyle\sum}\frac{1}{p^{3s}}+\cdots\cdots\lt\overset{\infty}{\underset{n=2}{\textstyle\sum}}\left(\frac{1}{n^2}+\frac{1}{n^3}+\cdots\cdots\right)=\overset{\infty}{\underset{n=2}{\textstyle\sum}}\frac{1}{n\left(n-1\right)}=1.\]故に $\left(\ 9\ \right)$ と比較して,$s\rightarrow1$ のとき\[\overset{p}{\textstyle\sum}\frac{1}{p^s}\sim\log\frac{1}{\ s-1\ }.\]同様に\[L_K\left(s\right)=\overset{p}{\textstyle\prod}\frac{1}{1-\dfrac{\chi\left(p\right)}{p^s}}\]を取り扱えば,$s\rightarrow1$ のとき,$L_K\left(s\right)\rightarrow L_K\left(\ 1\ \right)=h\kappa$ であるから.\[\overset{p}{\textstyle\sum}\frac{\chi\left(p\right)}{p^s}\]は有限である.
$\chi\left(p\right)=0$ なる第三種の素数 $p$ は $d$ の約数に限る.それらを除いて $\chi\left(p\right)=\left(\dfrac{d}{p}\right)=\pm1$ である第一種と第二種との素数をそれぞれ $p$,$q$ で表わせば,$s\rightarrow1$ のとき\begin{alignat*}{1}{\textstyle\sum}\frac{1}{p^s}+{\textstyle\sum}\frac{1}{q^s}\rightarrow\infty,\\[2mm]{\textstyle\sum}\frac{1}{p^s}-{\textstyle\sum}\frac{1}{q^s}\rightarrow h\kappa,\end{alignat*}したがって\[\overset{p}{\textstyle\sum}\frac{1}{p^s}\rightarrow\infty,\hphantom{n}\overset{q}{\textstyle\sum}\frac{1}{q^s}\rightarrow\infty.\] 故に第一種の素数 $p$ も第二種の素数 $q$ もおのおの無数に存在する($\S\ 44$,$288$ 頁参照).