第 $3$ 章　スツルムの問題$\hspace{0.5mm}$，$\hspace{-0.5mm}$根の計算

　$\S\ 17.$　虚根に関する Sturm の問題

　$\boldsymbol{1.}$　$f(z)=0$ を任意の方程式とし，複素数平面上において与えられた単純な閉曲線（二重点をもたない閉曲線）$C$ の内部にあるその根の数を $N$ とすれば，$z$ が $C$ の周上を正の向きに（$C$ の内部を左に見ながら）一周するとき $\operatorname{arc}f(z)$ の増加が $2\pi\times N$ であることはすでに説明した通りである（定理 $2.\ 5$）．ただし $C$ の周上には $f(z)=0$ の根はないものと仮定しなければならない．またここでは，根の数 $N$ は複根の重複度数を数えていうのである．
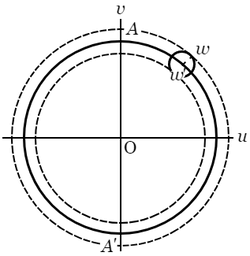
　上の $\operatorname{arc}f(z)$ の増加を求めるために，$f(z)$ を $w$ で表わし，\[w=u+vi\]とおいて，$z$ が $z_0$ から出発して $C$ を一周するときに，$w$ が $w$ 平面上において $w_0=f(z_0)$ から出て $w_0$ に帰るまでの通路 $K$ を考察する．$w$ が描く曲線は複雑であるが，いま標本の意味で次の図に示すような曲線とする．仮定によって $C$ の周上に $f(z)$ の根がないから，曲線 $K$ は $0$ を通らない．$w$ が $K$ の上を一周するときのベクトル $\overrightarrow{0w}$ の回転の純量が問題であるが，この純量を得るために，$w$ が $v$ 軸を横切るとき，すなわち $u$ が $0$ になる際に，$uv$ が $+$ から $-$ になる回数と，$-$ から $+$ になる回数とを数えよう．
　右の方の図に陰影で示すように，$w$ 平面の四つの象限の中，$uv$ が $+$ であるところと $-$ であるところとを白黒の二部に区別して，$v$ 軸を関所として $w$ の通路を監視する．$w$ が白から黒に入るときには白札，また黒から白へ出るときには黒札をもってそれを標記することにして，$w$ が一周を終わったときに，白札が黒札より何枚多いかを計算して，それを $\pi$ に掛けるならば，それがすなわちいま求めようとするところの回転の純量である．
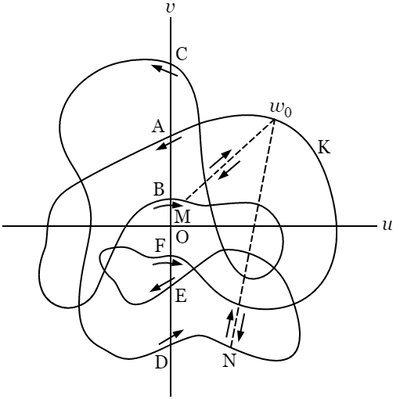　上の図の場合では，$K$ は $A$，$B$，$C$，$D$，$E$，$F$ において $6$ 回 $v$ 軸を横切るが，そのうち $A$，$C$，$D$，$F$ が白札，$B$，$E$ が黒札で，すなわち白が黒より $2$ 枚多いから，回転の純量は $2\pi$ である．
　さて，この計算法が実際に合うことを証明しなければならないが，まず $w$ は $w_0$ から出て $w_0$ に帰るのであるから，$v$ 軸を横切る回数は偶数でなければならない．そこで証明を見やすくするために，$w$ が $v$ 軸を $2$ 回横切るごとに，一まず任意の経路によって出発点 $w_0$ へ帰らせて，その上で更に同じ経路を辿ってもとの通路に戻って進行を続けさせることにしょう．図に点線で示した $Mw_0$，$Nw_0$ がそれらの経路である．$w$ が通路 $K$ に属さない余計の路を通っても，それは同じ路を行ってまたかえるのであるから，$\operatorname{arc}w$ の増減には影響がない．ゆえに通路 $K$ の代わりに $w_0ABMw_0$，$w_0MCDNw_0$，$w_0NEFw_0$ という三つの路に関する $\operatorname{arc}w$ の増加の総量を求めればよいことになる．さて，これらの路を単純化して描いて見れば次のようになる．

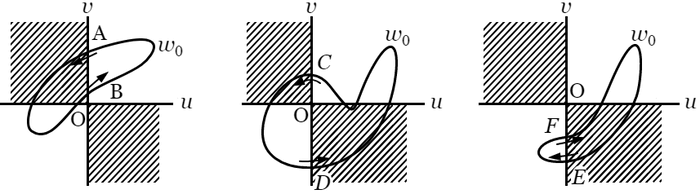　第一と第三とは $v$ 軸を横切る $2$ 回のうち $1$ 回が白札，$1$ 回が黒札で，すなわち二つの横断点は $0$ の同じ側にある．また第 $2$ では $2$ 回ともに白札で，すなわち二つの横断点は $0$ の反対の側にある．そこで第一の場合であるが，この場合に限ることではないけれども，閉曲線である路上のどの点を出発帰着の点としても，回転の純量に影響はないから，$w_0$ の代わりに $A$ を出発点として考えよう．そうすると，$w$ は $A$ を入ってから $B$ を出るまでは，常に $v$ 軸の左側にあるので，その間にどのような路を通ったとしても，$0w$ の回転の純量は $0$ である．また $B$ を出てから $A$ に帰るまでは，常に $v$ 軸の右側にあって，その間にも回転の純量は $0$ で，結局一周の結果は回転量 $0$ である．第三の場合も同様である．
　しかるに第二の場合には，$C$ から $D$ までの間に動径 $\overrightarrow{0w}$ は $v$ 軸の正の向きから出発して後，常に $v$ 軸の左側にあって，ついに $v$ 軸と負の向きに来るのであるから，この間の回転の純量は $+\pi$ である．また $D$ から $C$ に帰るまでの間においても，回転の純量はやはり $+\pi$ である．すなわち回転の総純量は $2\pi$ である（もしも $C$，$D$ がともに黒札ならば $-2\pi$）．
　$u$ が $0$ になる際に $uv$ が $-$ から $+$ に変わる場合（黒札）には $\chi=+1$ とし，$uv$ が $+$ から $-$ に変わる場合（白札）には $\chi=-1$ とおいて，前節の記法を襲用することにする．よってまた $u$ が $0$ になる際に $uv$ が符号を変えない場合には，$\chi=0$ とおく．この場合は，曲線 $K$ が $v$ 軸に触れるだけで，$v$ 軸を横切らないで，白からただちに白へ，または黒からただちに黒へ返るのであるから，上の考察において問題にする必要がなかったのである．
　このような記号を用いるならば，上の考察の結果を次のようにいい表わすことができる．
 〔定理 $\boldsymbol{3.\ 4}$〕 複素数平面上において，$z$ が単純な閉曲線 $C$ の周上を正の向きに一周するとき，$f(z)=u+vi$ とおいて $u$ が $0$ になる各々の場合における $\chi$ の総和を $\sum\chi$ とすれば，$C$ の内部における $f(z)=0$ の根の数 $N$（複根を数える）は次の式によって与えられる．\[N=-\frac{1}{2}{\textstyle\sum}\chi.\]　上の考察においては，$u$ が $0$ になる度数は有限と仮定したのである．後に述べる応用では，$w$ がある変数の多項式になる場合のみを取り扱うから，さしつかえない．
 〔例 $1$〕 最も簡単な例として\[f(z)=z^n\]で，$C$ は単位円周である場合を考察する．
　この場合には，$w=z^n$ が描く通路 $K$ は何であるか．$w$ は単位円周を正の向きに $n$ 回回転する．よって $w$ は $v$ 軸を $2n$ 回横切る．それはいつも白札である．よって $\sum\chi=-2n$．したがって，$(\ 1\ )$ によって $N=n$．単位円内に $z^n=0$ の根が $n$ 個ある．それは $n$ 重根 $z=0$ である．
 〔例 $2$〕 $f(z)=z^n+a_1z^{n-1}+\cdots+a_n$ として，$C$ は原点を中心とする半径 $R$ の円周であるとする．$z=Rz^\prime$ とすれば，$z^\prime$ は単位円を一周する．\[\frac{\ f(z)\ }{R^n}=z^{\prime\ n}+\frac{\ a_1\ }{R}z^{\prime\ n-1}+\frac{\ a_2\ }{R^2}z^{\prime\ n-2}+\cdots+\frac{\ a_n\ }{R^n}\]において，$\varepsilon$ を任意に小さい正数とするとき，$R$ を適当に大きくとれば，$|z^\prime|=1$ であるとき，右辺の第一項以下の絶対値を $\varepsilon$ よりも小さくすることができる．そこで\[\frac{\ f(z)\ }{R^n}=w,\hphantom{1}z^{\prime\ n}=w^\prime,　\frac{\ a_1\ }{R}z^{\prime\ n-1}+\cdots+\frac{\ a_n\ }{R_n}=w^{\prime\prime}　すなわち　w=w^\prime+w^{\prime\prime}\]とおけば，$z^\prime$ が単位円周を一周するとき，$w^\prime$ は単位円周を $n$ 回回転するが，$w=w^\prime+w^{\prime\prime}$ において $|w^{\prime\prime}|\lt\varepsilon$ であるから $w$ は単位円周の両側において $1\pm\varepsilon$ の半径をもつ二つの同心円によって限られる環内において変動する．$w^\prime$ が単位円周上を回転するときに，$w$ は $w^\prime$ から $\varepsilon$ 以内の距離にある衛星のように運動するのである．
　ゆえに $w^\prime$ が $A$ または $A^\prime$ において $v$ 軸を横切る前後において $w$ もまた $v$ 軸を横切るであろう．その際 $w$ は $1$ 回よりも多く $v$ 軸を横切るとしても，結局 $v$ 軸の一側から他側に移るのであるから，横断の度数は奇数で，かつ白札が黒札よりも必ず $1$ 個ずつ多いのである．
　ゆえに $\operatorname{arc}w$ の増加の純量は $\operatorname{arc}w^\prime$ と同じく $2n\pi$ でなければならない．したがって $|z|=R$ なる円内において $f(z)=0$ は $n$ 個の根をもつ．これすなわち代数学の基本定理である．
　$\boldsymbol{2.}$　曲線 $C$ が円周である場合，または一般に $C$ が有理曲線である場合には，上の回転純量の計算を定理 $3.\ 2$ に帰させることができる．有理曲線とは，その曲線上の点の座標 $(x,\ y)$ が一つの変数 $t$ の有理函数として表わされるものをいうのである．
　いま $C$ を $z_0=a+bi$ を中心とする半径 $r$ の円周とすれば，$z=x+yi$ において\[\begin{array}{cc}\begin{alignat*}{2}x&=a+r\cos\theta&&=a+r\frac{t^2-1}{t^2+1},\\[2mm]y&=b+r\sin\theta&&=b-r\frac{2t}{t^2+1},\end{alignat*}&\left(t=-\cot\dfrac{\theta}{2}\right)\end{array}\]すなわち\[z=z_0+r\frac{t^2-1-2ti}{t^2+1}\tag{$\ 2\ $}\]とおけば実変数 $t$ が $-\infty$ から $\infty$ まで変わるとき，$z$ は円周 $C$ を正の向きに一周する．これを $f(z)$ に代入して，実の部分と虚の部分とを分けて\[f(z)=\frac{\ \varPhi(t)+i\varPsi(t)\ }{(t^2+1)^n}\]とする．$n$ は $f(z)$ の次数で，$\varPhi(t)$，$\varPsi(t)$ は $t$ に関して $2n$ 次の多項式である．前に $u$，$v$ で表わしたものは\[u=\frac{\varPhi(t)}{(t^2+1)^n},\hspace{1cm}v=\frac{\varPsi(t)}{(t^2+1)^n}.\]　さて $t^2+1$ は常に正であるから，問題は $\varPhi(t)$ が $0$ になるとき，$\varPhi(t)\varPsi(t)$ が $-$ から $+$ に変わる回数と，$+$ から $-$ に変わる回数との差引勘定である．ゆえに $\varPhi(t)=0$ の実根を $t_0$ とすれば，定理 $3.\ 2$ から\[V(-\infty)-V(\infty)=\underset{t_0}{\textstyle\sum}\chi(t_0).\]よって定理 $3.\ 4$ から\[N=\frac{\ V(\infty)-V(-\infty)\ }{2}.\tag{$\ 3\ $}\]　$V$ は多項式 $\varPhi$，$\varPsi$ から $\S\ 15$ のように互除法によって求められる函数列における符号の変りの数で，$N$ は円 $C$ の内部にある $f(z)=0$ の根の数（複根の次数を数えて）である．
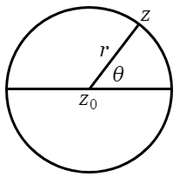　上の $\varPhi$，$\varPsi$ は $2n$ 次の多項式であるが，少し解法を変更して $n$ 次の多項式ですませることができる．
　$(\ 2\ )$ の右辺の分数を約して\[z=z_0+r\frac{\ t-i\ }{t+i}.\]　これを $f(z)$ に代入して\[f(z)=\frac{\ \varphi(t)+i\psi(t)\ }{(t+i)^n}\]とすれば，$\varphi(t)$，$\psi(t)$ は $n$ 次の多項式である．$z$ が $C$ の周上を一周するとき，$\operatorname{arc}f(z)$ の増加はすなわち $t$ が $-\infty$ から $+\infty$ まで変わるとき，右辺の数の $\operatorname{arc}$ の増加で，分母 $(t+i)^n$ の $\operatorname{arc}$ の増加は $-n\pi$ であるから，$\operatorname{arc}\{\varphi(t)+i\psi(t)\}$ の増加を求めることに帰す．それに $n\pi$ を加えて（$-n\pi$ を引いて）$\operatorname{arc}f(z)$ の増加が得られる．
　$\operatorname{arc}\{\varphi(t)+i\psi(t)\}$ の増加は $\varphi(t)$，$\psi(t)$ に関して記号 $\chi^{\ \prime}$ を前と同様の意味に用いるならば，$-\sum\chi^{\ \prime}\hspace{0.7mm}\cdotp\pi$ に等しい．
　この場合に，$w=\varphi+i\psi$ の描く曲線は閉曲線ではない．\[\varphi(t)=at^n+\cdots,\hspace{5mm}\psi(t)=bt^n+\cdots\]とすれば，$t=\pm\infty$ のとき，ベクトル $\overrightarrow{0w}$ は直線 $y/x=b/a$ の上に来る．$n$ が偶数ならば，$\overrightarrow{0w}$ の方向は，$t=-\infty$ のとき，$t=+\infty$ のときと同一になるから，$\overrightarrow{0w}$ の回転の総量は $\pi$ の偶数倍であるが，$n$ が奇数ならば，$\overrightarrow{0w}$ の方向は，$t=-\infty$ のときと，$t=+\infty$ のときと反対になるから，$\overrightarrow{0w}$ の回転の総量は $\pi$ の奇数倍である．


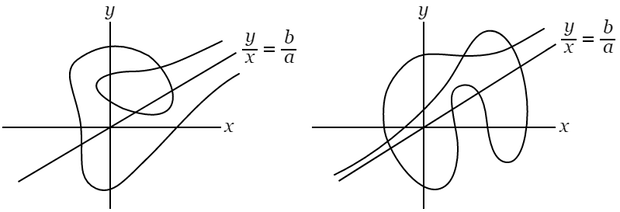　$\varphi+i\psi$ の描く通路が閉曲線でなくても，上の $\boldsymbol{1}$ の曲線 $K$ に関する考察は，そのまま適用されるのである．
　よって $\varphi(t)$，$\psi(t)$ に定理 $3.\ 2$ を適用して，符号の変りを $V$ で表わすならば\[V(-\infty)-V(\infty)={\textstyle\sum}\chi^{\ \prime}.\]　したがって\[N\hspace{0.7mm}\cdotp2\pi=(-{\textstyle\sum}\chi^{\ \prime}+n)\pi\]から\[N=\frac{\ V(\infty)-V(-\infty)+n}{2}\tag{$\ 4\ $}\]を得る．
　上の考察は実数軸の両側における根の数に関しても適用される．
 〔定理 $\boldsymbol{3.\ 5}$〕 $n$ 次の多項式 $f(z)$ の係数の実数部と虚数部とを分離して\[f(z)=\varphi(z)+i\psi(z)\]とおく．実数軸の上側および下側にある $f(z)$ の根の数を（複根を数えて）それぞれ $N$，$N^\prime$ とし，$\varphi(z)$，$\psi(z)$ から互除法によって得られる函数列から $V$ を求めるならば，\[N=\frac{1}{2}\{n+V(\infty)-V(-\infty)\},\hphantom{1}N^\prime=\frac{1}{2}\{n+V(-\infty)-V(\infty)\}.\tag{$\ 5\ $}\]　ただし，$f(z)$ は実根をもたないと仮定する．実根は $\varphi(z)$ と $\psi(z)$ との共通根として求められるから，それを取り除いておくのである．
 〔証〕 この場合，ベクトル $\overrightarrow{0w}$ の回転の総量 $-\sum\chi\pi$ は $(N-N^\prime)\pi$ に等しいから，$N-N^\prime=V(\infty)-V(-\infty)$．これと $N+N^\prime=n$ とから，$(\ 5\ )$ を得る．
　任意の直線，たとえば $\alpha$，$\beta$ を通る直線は\[z=\alpha+(\beta-\alpha)t\]によって実数軸に変換される．
　そこで $f(\alpha+(\beta-\alpha)t)=\varphi(t)+i\psi(t)$ とおいて，上の定理を適用すれば，この直線の両側における根の数が得られる．ただし，$N$ は $\alpha$ から $\beta$ への向きに関して，直線の左側にある根の数である．
 〔例 $1$〕 $\S\ 15.$（$85$ 頁）に掲げた例において，$z=it$ とすれば\begin{alignat*}{2}&\varphi=-3.22t^6+4.12t^4+7.25t^2-7.84,&\hspace{15mm}&\psi=-3.11t^3+1.88t,\\[2mm]&\varphi_1=-8.56t^2+7.84,&&\psi_2=+0.97t,\\[2mm]&\psi_3=-7.84.&&\end{alignat*}\[V(-\infty)=2,\hspace{5mm}V(\infty)=2,\hspace{5mm}N=N^\prime=3.\]　すなわち虚数軸の両側に三つずつの根がある．正根と負根とは各一つずつであったのだから（参照 $85$ 頁），実数部が正なる虚根と負なる虚根とが一組ずつある．
 〔例 $2$〕 $f(z)=0$ の根が全部実数軸の一側にあるときには，$\varphi(z)=0$，$\psi(z)=0$ の根は全部実根で，互いに隔離する．逆も成り立つ．
 〔解〕 これは $\S\ 12.$ に述べた Hermite の定理およびその逆である．$\S\ 12.$ では，初等の方法で証明をしたが，定理 $3.\ 5$ を応用すれば，証明は簡単である．すなわち次の通り．
　まず $f(z)$ の根がすべて実数軸の上側にあるならば，$N=n$（$n$ はもちろん $f(z)$ の次数である）．ゆえに $V(\infty)-V(-\infty)=n$．したがって $\varphi$，$\psi$ に関して $\sum\chi=-n$．ゆえに $\varphi=0$ の各根に関して $\chi=-1$．ゆえに $\varphi=0$ は $n$ 個の実根をもち，かつ $\psi$ の実根によって隔離される．
　逆に $\varphi$，$\psi$ の根が全部実根で，かつ互いに隔離するならば，$\varphi=0$ の各根に関して $\chi=+1$ または $\chi=-1$，したがって $\sum\chi=\pm n$，ゆえに $V(\infty)-V(-\infty)=\mp n$．したがって $N=0$ または $N=n$（$\S\ 16$，問題 $1$，$2$ 参照）．
 〔例 $3$〕 （Hurwitz の問題）実係数の方程式 $f(x)=0$ の根が全部虚数軸の左側にあるための条件は何か．
　この問題は $1895$ 年にスイスのある水力発電所の設計に際して必要を生じて，ある技師の依頼によって Hurwitz が解いたのであるが，それよりも前に，すでに Routh がある力学上の問題に関係して解決したものである．
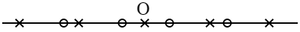　この問題は $x=iz$ とおけば，Hermite の問題（例 $2$）に帰する．$x$ の実数部が負であるとき，$z$ の虚数部は正になるから，$f(iz)=0$ の根が全部実数軸の上側にあるための条件を求めるのである．いま\[f(x)=a_0+a_1x+a_2x^2+\cdots+a_nx^n\]とすれば，$f(iz)=U(z)+iV(z)$ とおくとき\[U(z)=a_0-a_2z^2+a_4z^4-\cdots,\hspace{5mm}V(z)=z(a_1-a_3z^2+a_5z^4-\cdots).\]　条件はこの $U$，$V$ に関して $\sum\chi=-n$ になることである．ただし $U$，$V$ が $z$ の偶数冪または奇数冪だけを含むから，\[u(x)=a_0-a_2x+a_4x^2-\cdots,\hspace{5mm}v(x)=a_1-a_3x+a_5x^2-\cdots,\]とおいて，問題を簡約することができる．すなわち $u(x)$，$v(x)$ の根は全部正数で，互いに隔離し，かつ最小根は $u(x)$ に属し，また $u(x)$，$v(x)$ に関して常に $\chi=-1$ であることが条件である．後文（$\S\ 74.$ ）で再びこの問題に立ち返るであろう．
 〔例 $4$〕 $\mathrm{C}$ が二つ以上の有理曲線の断片を接合したものであるときにも，上の方法を適用することができる．たとえば $\mathrm{C}$ が右の図に示すように，軸に平行な辺をもった矩形であるとすれば，その各辺に応じて四組の $\varphi$，$\psi$ を要する．すなわち辺 $\mathrm{AB}$ に関しては\[f(x+a^\prime i)=\varphi_1(x)+i\psi_1(x)\hspace{1cm}(a\leqq x\leqq b)\]として，この $\varphi_1$，$\psi_1$ と区間 $a\leqq x\leqq b$ とに関して\[V_1(a)-V_1(b)={\textstyle\sum}_1\chi\]を求める．次に辺 $\mathrm{BC}$ に関しては\[f(b+yi)=\varphi_2(y)+i\psi_2(y)\hspace{1cm}(a^\prime\leqq y\leqq b^\prime)\]に対して\[V_2(a^\prime)-V_2(b^\prime)={\textstyle\sum}_2\chi\]を求める．同じようにして辺 $\mathrm{CD}$，$\mathrm{DA}$ に関しては\begin{alignat*}{1}&f(x+b^\prime i)=\varphi_3(x)+i\psi_3(x),&\hspace{1cm}&\hphantom{^\prime}(a\leqq x\leqq b),\\[2mm]&f(a+yi)=\varphi_4(y)+i\psi_4(y),&\hspace{1cm}&(a^\prime\leqq y\leqq b^\prime)\end{alignat*}とするのであるが，進行の方向が逆になるから，\[V_3(b)-V_3(a)=-{\textstyle\sum}_3\chi\hspace{8mm}V_4(b^\prime)-V_4(a^\prime)=-{\textstyle\sum}_4\chi\]よって，矩形内に含まれる根の数 $N$ は\[N=\frac{1}{2}\Bigl(-{\textstyle\sum}_1-{\textstyle\sum}_2+{\textstyle\sum}_3+{\textstyle\sum}_4\Bigr)\underset{.}{\ }\]