第 $3$ 章 スツルムの問題$\hspace{0.5mm}$,$\hspace{-0.5mm}$根の計算
$\S\ 21.$ Newton の方法
$\boldsymbol{1.}$ 区間 $(a,\ b)$ に $f(x)$ の根があることが知られ,かつその区間がすでに十分狭く取られて,区間内において $f^{\prime\prime}(x)$ が一定の符号をもつとするとき,次のようにして根の近似値を求めることができる.まず $f^{\prime\prime}(x)\gt0$ とし,$\alpha$ を $f(x)$ の根とする.$f^\prime(x)$ は単調に増大するから,もしも $f^\prime(\alpha)\lt0$ ならば,区間 $(a,\ \alpha)$ において $f^\prime(x)$ は常に負,したがって $f(x)$ は単調に減少する.ゆえに $f(a)\gt0$,$f^\prime(a)\lt0$.またもし $f^\prime(\alpha)\gt0$ ならば,$(\alpha,\ b)$ において $f^\prime(x)$ は常に正,したがって $f(x)$ は単調に増大するから $f(b)\gt0$,$f^\prime(b)\gt0$.
区間 $(a,\ b)$ に根が一つより多くあるときには,根の数は二つで,$f(a)$,$f(b)$ はともに正である($\S\ 20$,問題 $7$).
 |
同様に $f^{\prime\prime}(x)\lt0$ であるときには,$f(a)$ または $f(b)$ が負になる($f$ に $-f$ を代用して考える).
Newton の方法では,区間 $(a,\ b)$ の両端の中で $f$ と $f^{\prime\prime}$ との符号の一致する方を取って,それを根の第一の近似値と見なし,それから次々に一層精密な近似値を求めて行くのである.
いま $f^{\prime\prime}(x)\gt0$,$f(a)\gt0$(したがって $f^\prime(a)\lt0$,上出)として,その方法を説明する.
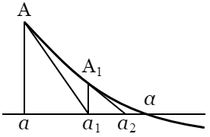 |
この接線の方程式は\[y=f(a)+f^\prime(a)(x-a)\]であるから,それが $x$ 軸に交わるところを $x=a_1$ とすれば,\[a_1=a-\frac{\ f(a)\ }{f^\prime(a)}.\]$f^\prime(a)\lt0$ だから,$a\lt a_1$.またグラフは上向きに弯曲しているから,$f(a_1)\gt0$.したがって $a_1\lt\alpha$.すなわち $a\lt a_1\lt\alpha$ であるから,$a_1$ は $a$ よりも $\alpha$ に近いのである.
次に $a$ に $a_1$ を代用して同様の計算を行なう.$x=a_1$ に対応するグラフの点を $\mathrm{A}_1(a_1,\ f(a_1))$ とし,$\mathrm{A}_1$ における接線が $x$ 軸に交わる点を $x=a_2$ とすれば\[a_2=a_1-\frac{\ f(a_1)\ }{f^\prime(a_1)},\hspace{1cm}a_1\lt a_2\lt\alpha.\] この操作を無限に続行するとすれば,$a\lt a_1\lt a_2\lt a_3\lt\cdots$ のように,しだいに増大する数の一列を得るが,それらは $\alpha$ よりも小であるから,ある一つの極限に近迫する.その極限を $\lambda$ とすれば,$\lambda\leqq\alpha$ であるが,\[a_{n+1}=a_n-\frac{\ f(a_n)\ }{f^\prime(a_n)},\]であるから,\[\lambda=\lambda-\frac{\ f(\lambda)\ }{f^\prime(\lambda)}.\] ゆえに $f(\lambda)=0$.したがって $\lambda=\alpha$(区間 $(a,\ \alpha)$ に $f(x)$ の他の根はないから).
すなわち $a_n\rightarrow\alpha$.ゆえに $a_1$,$a_2$,$a_3$,$\cdots$ は限りなくしだいに $\alpha$ に近迫する.これが Newton の方法の理論的の根拠である.
$\boldsymbol{2.}$ 次の例は Newton が取り扱ったものである.
| 〔例〕 | \[f(x)=x^3-2x-5=0.\hspace{1cm}\tag{$\ 1\ $}\] |
| $f^\prime(x)=3x^2-2,\hspace{8mm}f^{\prime\prime}(x)=6x.$ | |
Descartes の符号律によって正根が一つある.いまその正根を計算しよう.$f(2)=-1$ であるから,根は $2$ よりも大きいが,$f(2)$ が小さいから,根は $2$ に近いであろう.
| $1\hphantom{11.}$ | $0\hphantom{11}$ | $-2\hphantom{111}$ | $-5$ | |
| $2.1$ | $\hphantom{-}4.41$ | $\hphantom{-}5.061$ | ||
| $2.1$ | $\hphantom{-}2.41$ | $\hphantom{-}0.061$ | ||
| $2.1$ | $\hphantom{-}8.82$ | |||
| $4.2$ | $\ 11.23$ | |||
| $2.1$ | ||||
| $1$ | $6.3$ | |||
ここでは $f^{\prime\prime}\gt0$,$f(2.1)\gt0$.ゆえに $a=2.1$ として計算を始める.根は $a$ よりも小さいから $u=a-x=2.1-x$ とおいて,$u$ を正にするのである.
さて\[0.061-11.23u=0\]から $u$ の近似値として\[\frac{\ 0.061\ }{11.23}=0.00543188\cdots\tag{$\ 3\ $}\]を得る.
いまその最高位一桁だけを取って $u=0.005+v$.
すなわち\[x=2.1-0.005-v\]とおいて,前のように $(\ 2\ )$ に代入して $v$ の昇冪に排列し,次々にこのようにして,根の数字を一桁ずつ求めて行くことができる.
このように Newton の方法を根の計算に応用するのを Horner の方法という.計算は次の通り.
| $\hphantom{1}1\hphantom{11}$ | $-6.3$ | $\hphantom{-}11.23$ | $-0.061$ | |||||||||
| $\hphantom{-}0.005$ | $-\hphantom{1}0.031475$ | $+0.055992625$ | $\hphantom{000}0.005$ | |||||||||
| $-6.295$ | $\hphantom{-}11.198525$ | $-0.005007375$ | ||||||||||
| $\hphantom{-}0.005$ | $-\hphantom{1}0.031450$ | |||||||||||
| $-6.290$ | $\hphantom{-}11.167075$ | |||||||||||
| $\hphantom{-}0.005$ | ||||||||||||
| $-6.285$ | ||||||||||||
| $(^{\ \large*\ })\hphantom{1}$ | $\hphantom{1}1$ | $-6.29$ | $\hphantom{-}11.16708$ | $-0.005007375$ | $\hphantom{000}0.0004$ | |||||||
| $\hphantom{-}0$ | $-\hphantom{1}0.00252$ | $+0.004465824$ | ||||||||||
| $-6.29$ | $\hphantom{-}11.16456$ | $-0.000541551$ | ||||||||||
| $-\hphantom{1}0.00252$ | ||||||||||||
| $\hphantom{-}11.16204$ | ||||||||||||
| $(^{\large**})$ | $\hphantom{1}1$ | $-6.3$ | $\hphantom{-}11.1620$ | $-0.000541551$ | $\hphantom{000}0.00004$ | |||||||
| $\hphantom{-}0$ | $-\hphantom{1}0.0003$ | $+0.000446468$ | ||||||||||
| $\hphantom{-}11.1617$ | $-0.000095083$ | $\hphantom{000}0.000008518$ | ||||||||||
| $\hphantom{-0.0000}89294\hphantom{1}$ | ||||||||||||
| \begin{alignat*}{1}\\u&=0.005448518\\[2mm]x&=2.094551482\end{alignat*} |
| |||||||||||
上の $(^{\ \large*\ })$ のところは $v$ を求める方程式の係数であるが,根を定数項と同じく小数第九位あたりまで求めるつもりで,第二,第三の係数の末位を四捨五入しておいたのである.その定数項を第三の係数で割って(符号を変えて)根の次の位として $0.0004$ を得る.それを用いて $v=0.0004+w$ とおいて,$w$ の方程式を求めるのであるが,その際,第三の数は末位(小数第 $5$ 位)未満を四捨五入しつつ計算すれば,結果は $(^{\large**})$ のようになる.よって根の次の位 $0.00004$ を得るが,これを用いて同様の省略をしながら次の段に移るとして,もはや第三の係数が根の次位以下の数字のために影響を受けないから,省略割算によって根の数字四桁を求めるのである.
根の末位はやや不確かであるが,参考として残しておく.
このような省略をしないでは,Horner の方法は実用に適しないであろう.
$\boldsymbol{3.}$ 上の例の $x=2.1$ のように,すでに根に近い値が得られたときには,Horner 式の計算によらないで,逐次補正の法によって根の近似値を迅速に求めることができる.
上の $(\ 2\ )$ から\[u=\frac{\ 0.061\ }{11.23}+\frac{\ u^2(6.3-u)\ }{11.23},\tag{$\ 4\ $}\]ゆえに $u$ の代わりに $(\ 3\ )$ の値を取れば,誤差は\[\frac{\ u^2(6.3-u)\ }{11.23}\tag{$\ 5\ $}\]に等しい.$u$ の値は知れていないけれども,$(\ 3\ )$ がそれに近いから,それを用いて,$(\ 5\ )$ から誤差を概算することができる.すなわち\[u=\ \!\!約\ 5\times10^{-3},\hspace{5mm}u^2=\ \!\!約\ 30\times10^{-6},\hspace{5mm}(\ 5\ )=\ \!\!約\ 2\times10^{-5}.\] ゆえに $(\ 3\ )$ によって,$u=0.0054$ とすれば,末位まで正しいが,上の $(\ 5\ )$ を入れていま一桁多くとれば,\[u=\ \!\!約\ 0.00545.\tag{$\ 6\ $}\]これを用いて $(\ 5\ )$ を四桁だけ計算すれば\[0.00001665\tag{$\ 7\ $}\]を得る.これを $(\ 3\ )$ に加えて\[u=0.00544853\tag{$\ 8\ $}\]とすれば,一層よい.しからば\[x=2.09455147\]を得る.
$(\ 8\ )$ によれば $(\ 6\ )$ の値には $1$ 万分の $3$ ほどの比例誤差があるから,$(\ 7\ )$ の末位は不確かで,したがって $(\ 8\ )$ の末位も不確かである(前掲の結果と比較せよ).
代数書に Horner の方法を記載することが慣例になっているから,本書にも一例を掲げておくのであるが,すべて近似計算では計算尺,計算器および各種の表または図解法を用いるのであって特別の修練を要する.器械なしの紙上計算は実用的でない.また代数方程式の根の近似計算だけを切り離して取り扱うことは不適切であるから,本書では上の一例を以て近似計算は打ち切る.