第 $5$ 章 対 称 式$\hspace{0.5mm}$,$\hspace{-0.5mm}$置 換
$\S\ 30.$ 置 換
$\boldsymbol{1.}$ 相異なる $n$ 個の物を一つの順序から他の順序におき換えることを置換という.ここで置換の卑近な二,三の性質について解説を試みるに当たって,置換される物に適宜に $1$,$2$,$3$,$\cdots$,$n$ の番号をつけて,これらの物をその番号で示すことにする.$n$ 個の物を $n!=1\hspace{0.7mm}\cdotp2\hspace{0.7mm}\cdotp3\hspace{0.7mm}\cdotp\cdots n$ の相異なる順列に並べることができて,置換によって $1\ 2\ 3\ \cdots\ n$ なる順列から任意の順列に移ることができるから,置換の総数は $n!$ である.ただしこの中にはいわゆる恒等置換をも数える.すなわち各々の物を元のままの位置において少しも移動させない場合も,やはり一つの置換と見なすのである.
置換の記法は次のようにする.たとえば $12345$ を $35214$ にする置換を\[P=\left(\begin{array}{c}12345\\[1mm]35214\end{array}\right)\]としるす.上がもとの順列で,下が置換を行なった後の順列である.もし上の列と下の列とを交換すれば,それは逆の置換を表わすのである.上のように,置換を一つの文字 $P$ で表わすならば,その逆の置換を $P^{-1}$ で表わす,すなわち\[P^{-1}=\left(\begin{array}{c}35214\\[1mm]12345\end{array}\right).\]またはこれを次のようにしるしても同じことである.\[P^{-1}=\left(\begin{array}{c}12345\\[1mm]43152\end{array}\right).\]これは上の列が番号順になるように,上下に重なった $5$ 組の数字を並べかえたまでである.
$\boldsymbol{2.}$ 置換 $P$ を行なった後,更に置換 $Q$ を行なうならば,その効果はある一つの置換と同じである.その置換を $R$ とするとき,この関係を次のようにしるす.\[PQ=R.\] このようにして置換 $P$,$Q$ から置換 $R$ を作ることを置換の結合という.
たとえば\[P=\left(\begin{array}{c}12345\\[1mm]35214\end{array}\right),\hspace{7mm}Q=\left(\begin{array}{c}12345\\[1mm]41523\end{array}\right)\]ならば,\[PQ=\left(\begin{array}{c}12345\\[1mm]53142\end{array}\right).\]$1$ は $P$ によって $3$ でおき換えられ,その $3$ は $Q$ によって $5$ でおき換えられるから,結局 $1$ は $5$ でおき換えられる.ゆえに $PQ$ においては,$1$ の下に $5$ が来る.その他も同様である.
置換の結合においては,交換の法則は一般に成り立たない.すなわち $PQ$ と $QP$ とは同一でない.たとえば上の例で\[QP=\left(\begin{array}{c}12345\\[1mm]13452\end{array}\right)\neq PQ\] 結合の法則は置換にも当てはまる,すなわち $(AB)C=A(BC)$.よって括弧を略して $ABC$ としるす.三つより多くの置換に関しても同様である.
いま置換 $A$ によって,数字 $p$ が $q$ でおき換えられ,その $q$ が $B$ によって $r$ でおき換えられ,$r$ が $C$ によって $s$ でおき換えられるとする.しからば,$AB$ によって,$p$ が $r$ でおき換えられるから,$(AB)C$ によって,$p$ は $s$ でおき換えられる.一方,$p$ は $A$ で $q$ に換わり,$q$ は $BC$ で $s$ に換わるから,$p$ は $A(BC)$ によって,やはり $s$ でおき換えられる.どの文字 $p$ に関しても同様だから,$(AB)C=A(BC)$.
同一の置換をいくつも結合する場合には,冪の記法を襲用する.たとえば $PP=P^2$,$PPP=P^3$,など.
| 〔問題 $\boldsymbol{1}$〕 | $\vphantom{\frac{1}{1}}(AB)^{-1}=B^{-1}A^{-1}$, | |
| $(ABC)^{-1}=C^{-1}B^{-1}A^{-1}$,など. |
| 〔解〕 | $\vphantom{\frac{1}{1}}(AB)(B^{-1}A^{-1})$ | $=A(BB^{-1})A^{-1}$ | 結合法則による. |
| $=AA^{-1}$ | $BB^{-1}$ は恒等置換だから. | ||
| $\vphantom{\frac{1}{1}}=1.$ | $1$ は恒等置換を表わす. |
〔注意〕 $A^p$ すなわち $AA\cdots A$(因子 $p$ 個)の逆は $A^{-1}A^{-1}\cdots A^{-1}$ すなわち $(A^{-1})^p$ である.これを $A^{-p}$ としるす.これは $A$ の $p$ 乗の逆であるが,$A$ の逆の $p$ 乗でもある.どちらも同じである.
よってまた $A^0$ は恒等置換を表わすものとして,冪の記法を指数が $0$ および負の整数である場合に拡張する.しからば,一般に\[A^pA^q=A^{p+q},\hspace{7mm}(A^p)^q=A^{pq}.\]ただし,二つ以上の置換に関して,一般に\[(AB)^p\neq A^pB^p.\] たとえば,$(AB)^2=ABAB$ で $BA\neq AB$ ならば,これは $A^2B^2$ とは等しくない.前頁の例の $P$,$Q$ でためして見るとよい.
$\boldsymbol{3.}$ $n$ 個の物の中二つ,たとえば $a$,$b$ だけの位置を交換して,その他の物は動かさないような置換を特に互換といい,それを $(a,\ b)$ で表わす.
たとえば\[(12)=\left(\begin{array}{c}1234\cdots n\\[1mm]2134\cdots n\end{array}\right).\] すべて置換を互換の結合によって作ることができる.
たとえば\[A=\left(\begin{array}{c}12345\\[1mm]35214\end{array}\right)\]は $12345$ を $35214$ でおき換えるのであるが,まず $3$ を第一の位置へ来させるために $12345$ に互換 $(13)$ を行なえば $32145$ を得るから,この互換と置換\[\left(\begin{array}{c}32145\\[1mm]35214\end{array}\right)\]とを結合すれば,置換 $A$ を得る.しかるに後の置換では,$3$ が動いていないから,これは四つの物 $1245$ の置換である.よってこれを同様に扱かって,ついに $A$ を互換に分解することができる.
結果は次のようになる.
| $A=(13)(25)(12)(14)$ | $12345$ | |
| $(13)\hphantom{1}32145$ | ||
| $(25)\hphantom{1}35142$ | ||
| $(12)\hphantom{1}35241$ | ||
| $(14)\hphantom{1}35214$ |
たとえば上の例で,まず $(45)$ を行なって,$4$ を最後の位置に来るようにしてもよい.また互換の数をなるべく少なくすることを目的としないならば,途中で任意の互換を行なうこともできる.\begin{alignat*}{1}A&=(45)(15)(23)(35).\\[2mm]A&=(23)(15)(34)(14)(35)(15).\end{alignat*} このように,与えられた置換を互換に分解する仕方は限りなくあるが,その結果において,互換の数が奇数であるかまたは偶数であるかは,一定である.
これを証明するのに $\S\ 27$ の多項式($146$ 頁)\begin{alignat*}{1}P=(x_1-x_2)(x_1-x_3)\cdots(x_1-x_n)&\\[2mm](x_2-x_3)\cdots(x_2-x_n)&\\[2mm]\huge\cdotp\hspace{3mm}\cdotp\hspace{3mm}\cdotp\hspace{3mm}\cdotp\hspace{3mm}\cdotp\hspace{3mm}\cdotp\hspace{3mm}\cdotp&\\(x_{n-1}-x_n)&\end{alignat*}の性質を利用することにしよう.すなわち置換によって動かされるものは $n$ 個の変数 $x_1$,$x_2$,$\cdots$,$x_n$ であるが,ここでは,その番号だけに着眼すればよい.$n$ 個の変数に任意の置換を行なうときに,多項式 $P$ はまったく変わらないか,または $-P$ に変わるかであるから,置換は $P$ を変えないものと,$P$ を $-P$ に変えるものとの $2$ 種類に分かれる.しかるに $\S\ 27$ にいった通り,$P$ は二つの変数を互換するごとに,その符号を変えるから,$P$ を変えない置換は偶数の互換の結合であることを要し,$P$ を $-P$ に変えるものは奇数の互換の結合でなければならない.
同時にまたこれら $2$ 種の置換を区別する規準が得られる.いま一つの順列において大きい数字が小さい数字の前にあることを順位の反転と名づけることにする.
たとえば,順列 $35214$ では $3$ よりも小さい番号 $1$,$2$ が $3$ の後にあるから,そこに二つの反転があり,また $5$ と $2$,$1$,$4$ との間に三つの反転,$2$ と $1$ との間に一つの反転があり,すなわち合わせて $6$ 個の反転がある.
さて $1\ 2\ 3\ \cdots\ n$ に一つの置換を行なうときに生ずる反転の数が偶数ならば,その置換を上の多項式 $P$ に行なえば,因子の中で符号の変わるものが偶数個であるから,その置換は $P$ を変えないが,もし反転の数が奇数ならば,その置換は $P$ を $-P$ に変える.すなわち互換の数の奇数,偶数であるのと,順列中の反転の数の奇数,偶数であるのと同一である.
これによって $n!$ 個の置換を偶の置換と奇の置換とに区別する.
これら $2$ 種類の置換の数は相等しい.すなわち各々 $n!/2$ である.
それを見るには,すべての偶の置換を列挙したと想像して,それらにある一定の互換,たとえば $(1,\ 2)$ を結合するならば,その結果は相異なる同数の奇の置換であるから,偶の置換の数は奇の置換の数よりも多くはない.また同様に奇の置換の数は偶の置換の数よりも多くはないから,双方同数でなければならない.
以上を総合して次の定理を得る.
〔定理 $\boldsymbol{5.\ 4}$〕 $n$ 個の物の置換 $n!$ 個の中,半数は偶の置換で,半数は奇の置換である.前者は互換の結合で,$1,2,3,\cdots,n$ の間に偶数の反転を生ずる.それを多項式 $P$ の変数に行なうときは,$P$ は変わらない.後者は奇数個の互換の結合で,$1,2,3,\cdots,n$ の間に奇数の反転を生じ,$P$ を $-P$ に変える.
同種の置換二つを結合すれば偶の置換を生じ,異種の置換二つを結合すれば奇の置換を生ずる.二つ以上の置換を結合するとき,それらの置換の中に奇の置換が奇数個あるときに限って,結果が奇の置換である.
任意の置換は互換の結合によって作られるから,一つの多項式が対称式であることを確かめるのに,$n$ 個の変数を $n!$ 個の仕方でおき換えて見るまでもなく,変数を二つずつ互換して,その都度多項式が変わらないことを確かめれば十分である.しかるに,その手数を更に節約することができる.それは次の事実に基づく.
すべて互換,したがってすべての置換は,ある一定の一つの番号,たとえば $1$,を含む $n-1$ 個の互換 $(1,\ 2)$,$(1,\ 3)$,$\cdots$,$(1,\ n)$ から結合によって作ることができる.\[(a,\ b)=(1,\ a)(1,\ b)(1,\ a)\] $1ab$ は $(1,\ a)$ によって $a1b$ になり,それが $(1,\ b)$ によって $ab1$ になり,それに $(1,\ a)$ を行なえば $1ba$ になる.すなわち $1$ は結局元の位置にもどり,$a$ と $b$ とがその位置を交換するのである.
ゆえに変数 $x_1$,$x_2$,$\cdots$,$x_n$ の多項式が $x_1$ と他の変数とを互換しても変わらないならば,その多項式は対称式である.
〔例〕 $(x_1+x_2-x_3-x_4)(x_1-x_2+x_3-x_4)(x_1-x_2-x_3+x_4)$ は $x_1$,$x_2$,$x_3$,$x_4$ の対称式である.それを見るには,$(x_1,\ x_2)$,$(x_1,\ x_3)$,$(x_1,\ x_4)$ を互換して見ればよい.
$\boldsymbol{4.}$ 循環置換というのは,$a$,$b$,$c$,$\cdots$,$k$,$l$ なる物があるときに,$a$ を $b$ で,$b$ を $c$ で,$\cdots$,$k$ を $l$ で置き換え,最後の $l$ を最初の $a$ で置き換えるもので,それを $(abc\cdots kl)$ としるす.\begin{alignat*}{2}\left(\begin{array}{c}abc\cdots kl\\[1mm]bcd\cdots la\end{array}\right)&=(abc\cdots kl)&&=(bc\cdots kla)=\cdots\\[2mm]&=(klabc\cdots)&&=(labc\cdots).\end{alignat*}
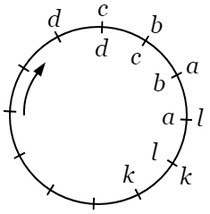 |
たとえば,\[P=\left(\begin{array}{c}123456789\\[1mm]458923167\end{array}\right)\]において,$1$ は $4$ で置き換えられ,その $4$ は $9$ で,また $9$ は $7$ で,$7$ は $1$ でおき換えられる.すなわち $1,4,9,7$ が循環的におき換えられる.この中に含まれない $2$ から始めて同様に $2,5$ なる環を得,また残りの $3$ から始めて $3,8,6$ なる環を得るから,結局\[P=(1497)(25)(386).\]また\begin{alignat*}{1}\left(\begin{array}{c}123456789\\[1mm]345678912\end{array}\right)&=(135792468).\\[2mm]\left(\begin{array}{c}123456789\\[1mm]963218547\end{array}\right)&=(1975)(2684)(3).\end{alignat*}この例では $3$ は移動しない.それは $3$,一個で一つの環を作るものと見なしてもよく,また $(\ 3\ )$ はしるさなくてもよい.
〔問題 $\boldsymbol{2}$〕 $(abc\cdots kl)=(ab)(ac)\cdots(ak)(al)$.
〔問題 $\boldsymbol{3}$〕 偶の置換は三つの物の循環置換の結合によって,しかも二つの特定の物,たとえば $1$,$2$ を含むもののみからの結合によって作られる.
〔解〕 偶の置換は $(12)$,$(13)$,$\cdots$.$(1n)$ の偶数個の結合である.さて\[(1a)(1b)=(1a)(12)(12)(1b)=(1a2)(12b).\hspace{1cm}(問題\ 2)\] 〔問題 $\boldsymbol{4}$〕 置換 $P$ が $k_1$ 個,$k_2$ 個,$\cdots$,$k_n$ 個の相異なる物の循環置換に分解されるならば,$P$ は $\sum k-n$ 個の互換に分解される.これが $P$ を合成する互換の最小数である.
〔解〕 初めの部分は問題 $2$ から直ぐに出る.後の部分は\begin{alignat*}{1}&(a_1a_2\cdots a_m)(a_1a_h)=(a_1a_2\cdots a_{h-1})(a_ha_{h+1}\cdots a_m)\\[2mm]&(a_1a_2\cdots a_m)(b_1b_2\cdots b_p)(a_mb_1)=(a_1a_2\cdots a_{m-1}b_1b_2\cdots b_pa_m)\end{alignat*}から出る.すなわち\[P=Q(ab)\]とするとき,$a$,$b$ が $P$ において同一の環に属するか,または相異なる環に属するかにしたがって $\sum k-n$ なる数は,$Q$ において $P$ におけるよりも $1$ だけ減り,または $1$ だけ増す.