第 $8$ 章 行 列 式
$\S\ 44.$ 行 列 式 の 定 義
前節では $(\ \text{I}\ )$ $(\ \text{II}\ )$ の性質をもつ整式 $\varDelta$ の存在を仮定したのであるが,いまこのような整式が果たして実際存在するかどうかの問題を解決せねばならない.前の通り $n$ 組の変数は相異なる $n$ 個の文字 $a$,$b$,$c$,$\cdots$,$l$ で表わし,各組における $n$ 個の変数はその文字に $1$,$2$,$\cdots$,$n$ なる番号をつけて区別することにする.さて $(\ \text{I}\ )$ によって $\varDelta$ は各組の変数に関して斉次一次式であるべきであるから,$\varDelta$ の各項は $a$,$b$,$c$,$\cdots$,$l$ なる文字を一つずつ含まねばならない.すなわち $\varDelta$ は $a_\alpha b_\beta c_\gamma\cdots l_\lambda$ のような積にある係数を掛けた項の和でなければならない.すなわち\[\varDelta={\textstyle\sum}Ca_\alpha b_\beta c_\gamma\cdots l_\lambda.\tag{$\ 1\ $}\]ただし $\alpha$,$\beta$,$\gamma$,$\cdots$,$\lambda$ は各々 $1$ ないし $n$ の番号を示すのである.
さて $(\ \text{II}\ )$ の条件から生ずる結果を考察するために,$n$ 種の文字の中の任意の二つ,たとえば $a$,$b$ に関して $\varDelta$ の項を括って,次のようにしるす.\[\varDelta=P_{11}a_1b_1+P_{12}a_1b_2+P_{21}a_2b_1+\cdots+P_{\alpha\alpha}a_\alpha b_\alpha+P_{\alpha\beta}a_\alpha b_\beta+P_{\beta\alpha}a_\beta b_\alpha+\cdots\]ここで係数 $P$ は $a$,$b$ 以外の文字 $c$,$\cdots$,$l$ のみを含むものである.$(\ \text{II}\ )$ によれば,$a_1=b_1$,$a_2=b_2$,$\cdots$,$a_n=b_n$ とするとき,$\varDelta$ は $0$ になるから,\[0=P_{11}a_1{}^2+(P_{12}+P_{21})a_1a_2+\cdots+P_{\alpha\alpha}a_\alpha{}^2+(P_{\alpha\beta}+P_{\beta\alpha})a_\alpha a_\beta+\cdots.\]しかもこれは $a_1$,$a_2$,$\cdots$,$a_n$ に関して恒等式であることを要するのであるから\[P_{\alpha\alpha}=0,\hphantom{1}P_{\alpha\beta}+P_{\beta\alpha}=0 \style{font-family:serif}{\text{すなわち}} P_{\beta\alpha}=-P_{\alpha\beta}.\hspace{1cm}(\alpha\neq\beta)\]$P_{\alpha\alpha}=0$ は $a_\alpha b_\alpha c_\gamma\cdots l_\lambda$ のように $2$ 種の文字 $a$,$b$ に同一の番号のついているような項が $\varDelta$ の中に含まれていてはならないことを示すものである.それは任意の二つの文字に関して,そうあらねばならないのであるから,実際 $\varDelta$ を組立てている項は $(\ 1\ )$ において $\alpha$,$\beta$,$\gamma$,$\cdots$,$\lambda$ なる番号がみな相異なるもののみで,すなわち $\alpha$,$\beta$,$\gamma$,$\cdots$,$\lambda$ は $1$,$2$,$3$,$\cdots$,$n$ の順列でなければならない.
次に $P_{\beta\alpha}=-P_{\alpha\beta}$ は\[a_\alpha b_\beta c_\gamma\cdots l_\lambda,\hspace{1cm}a_\beta b_\alpha c_\gamma\cdots l_\lambda\]のように,二つの文字 $a$,$b$ の番号だけが互換されている二つの項は符号だけの異なる係数をもたねばならないことを示す.それは任意の二つの文字に関してそうなるのであるから,いま $\varDelta$ が\[Ca_1b_2c_3\cdots l_n\]なる項を含むとすれば,この項から二つの番号の互換を偶数回行なって得られる項の係数はすべて $+C$ で,互換を奇数回行なって得られる項の係数はすべて $-C$ でなければならない.ゆえに結局 $\varDelta$ は次のような形をもたねばならない.\[\varDelta=C{\textstyle\sum}\pm a_\alpha b_\beta c_\gamma\cdots l_\lambda\]ここで $\alpha$,$\beta$,$\gamma$,$\cdots$,$\lambda$ は $1$,$2$,$3$,$\cdots$,$n$ の順列で,$\pm$ はその順列が偶類であるか奇類であるかにしたがって $+$ または $-$ である($\S\ 30$).
$\varDelta$ が前節 $(\ \text{I}\ )$ $(\ \text{II}\ )$ の二つの性質を備える以上,その形は上の通りでなければならないのであるが,逆に上の $\varDelta$ は実際 $(\ \text{I}\ )$,$(\ \text{II}\ )$ の性質をもつことは明白である.まず $(\ \text{I}\ )$ については論はない.また $\varDelta$ において二つの文字たとえば $a$,$b$ の番号だけが互換されている項\[a_\alpha b_\beta c_\gamma\cdots l_\lambda,\hspace{1cm}a_\beta b_\alpha c_\gamma\cdots l_\lambda\]は反対の符号をもつから $a_1=b_1$,$a_2=b_2$,$\cdots$,$a_n=b_n$ とするとき,二つずつ消し合って,$\varDelta$ は $0$ になる.$a$,$b$ の代わりに任意の二つの文字を取っても同様である.
| $\begin{vmatrix}a_1&b_1&c_1&\cdotp&l_1\\[1mm]a_2&b_2&c_2&\cdotp&l_2\\[1mm]a_3&b_3&c_3&\cdotp&l_3\\[1mm]\cdotp&\cdotp&\cdotp&\cdotp&\cdotp\\[1mm]a_n&b_n&c_n&\cdotp&l_n\end{vmatrix}$ |
これを $n$ 次の行列式といい,$a_1$,$\cdots$,$l_n$ なる $n^2$ 個の文字をその組成分子という.
また左の上から右の下への対角線(第一対角線という)の上にある組成分子の積である $a_1b_2c_3\cdots l_n$ を行列式の首項という.
たとえば\[\begin{vmatrix}a_1&b_1\\[1mm]a_2&b_2\end{vmatrix}=a_1b_2-a_2b_1\hspace{15mm}\begin{vmatrix}a_1&b_1&c_1\\[1mm]a_2&b_2&c_2\\[1mm]a_3&b_3&c_3\end{vmatrix}\begin{array}{l}=a_1b_2c_3+a_2b_3c_1+a_3b_1c_2\\[2mm]\hphantom{=}-a_1b_3c_2-a_2b_1c_3-a_3b_2c_1.\end{array}\] 上の三次行列式の展開を記憶するには,次のように行列式の三縦列に第一列と第二列とを添えてしるし,実線上にある左上から右下への三文字の積には符号 $+$ をつけ,破線上にある左下から右上への $3$ 文字の横には $-$ 符号をつけるようにするがよい.
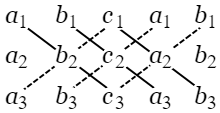 |