第 $9$ 章 二 次 形 式
$\S\ 65.$ 直 交 変 形
$\boldsymbol{1.}$ $n$ 個の変数の平方の和 $\displaystyle\overset{n}{\underset{\mu=1}{\textstyle\sum}}x_\mu{}^2$ を同じく平方の和 $\displaystyle\overset{n}{\underset{\mu=1}{\textstyle\sum}}x_\mu{}^{\prime\ 2}$ に変形するような,実係数の一次変形\[(x)=P(x^\prime)\]を直交変形という.解析幾何学において,一つの直交軸から同原点の他の直交軸に移る場合における座標の変換は,直交変形である.上記は,この幾何学的変換を $n$ 次元に拡張したもので,直交変形という称呼も,それに基づくのである.
直交変形の係数を $p_{\mu\nu}$ で表わして\begin{alignat*}{1}x_\mu&=p_{\mu1}x_1{}^\prime+p_{\mu2}x_2{}^\prime+\cdots+p_{\mu n}x_n{}^\prime\\[2mm]&\hphantom{=}(\mu=1,\ 2,\ \cdots,\ n)\end{alignat*}とする.しからば,上の定義によって次の恒等式が成り立つ.\[\overset{n}{\underset{\mu=1}{\textstyle\sum}}(p_{\mu1}x_1{}^\prime+p_{\mu2}x_2{}^\prime+\cdots+p_{\mu n}x_n{}^\prime)^2\equiv\overset{n}{\underset{s=1}{\textstyle\sum}}x_s{}^{\prime\ 2}.\] ゆえに\[\overset{n}{\underset{\mu=1}{\textstyle\sum}}p_{\mu\alpha}{}^2=1,\hspace{1cm}\overset{n}{\underset{\mu=1}{\textstyle\sum}}p_{\mu\alpha}p_{\mu\beta}=0.\hspace{1cm}(\alpha\neq\beta)\tag{$\ 1\ $}\] すなわち直交変形の係数の行列 $P$ において,各列の組成分子の平方の和は $1$ に等しく,また二つの異なる列の同番号の組成分子の積の和は $0$ に等しい.
このような関係は定理 $9.\ 3$ によって,かつ行列の記法を応用するときに,次のようにはなはだ明白になる.
平方の和 $\sum\ \!x_\mu{}^2$ は係数が単位行列 $E$ なる二次形式である.ゆえに定理 $9.\ 3$ によれば,直交行列(直交変形の係数の行列)$P$ の定義を次のようにしるすことができる.\[P^\prime EP=E,\]あるいは\[P^\prime P=E.\tag{$\ 2\ $}\]この結合を実行すれば,上の等式 $(\ 1\ )$ が出る.
Kronecker にしたがって $E$ の組成分子を $\delta_{\alpha\beta}$ で表わす.すなわち $\delta_{\alpha\alpha}=1$,$\delta_{\alpha\beta}=0$($\alpha\neq\beta$).しからば $(\ 1\ )$ を次のようにしるすことができる.\[\overset{n}{\underset{\mu=1}{\textstyle\sum}}p_{\mu\alpha}p_{\mu\beta}=\delta_{\alpha\beta}.\tag{$1^{\large*}$}\] また $(\ 2\ )$ から\[|\ \!P\ \!|^2=1.\]ゆえに直交行列式は $\pm1$ に等しい.
この $\pm1$ の符号にしたがって,直交行列を正式の直交行列と非正式の直交行列とに区別する.
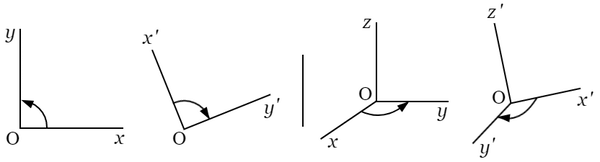
解析幾何学で,直交軸の変更から生ずる座標の直交変形は直交軸の向きが同一であるか,反対であるかにしたがって,正式または非正式の直交変形である(次の図は反対の向きを示す).
 |
また $(\ 3\ )$ から次の結果を得る.\[P_{\mu\nu}=\pm p_{\mu\nu}.\]$P_{\mu\nu}$ は $P$ における $p_{\mu\nu}$ の余因数で,$\pm$ は $|\ \!P\ \!|=\pm1$ の符号そのものである.
上記は直交行列の性質であるが,これから述べようとすることは実係数の二次形式を直交変形によって標準形式にするという問題である.すなわち解析幾何学における古典的の問題の $n$ 次元への拡張である.