第 $1$ 章 初 等 整 数 論
$\S\ 9.$ $1$ の $n$ 乗 根
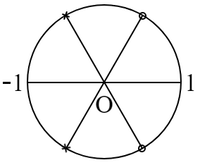
$\boldsymbol{1.}$ $1$ の $n$ 乗根すなわち,方程式 $x^n-1=0$ の根は $n$ 個あって,それらは\[\left.\begin{array}{l}\cos\theta+i\sin\theta,\\\theta=\dfrac{2k\pi}{n},\ \ k=0,\ 1,\ 2,\ \cdots\cdots,\ n-1.\end{array}\ \right\}\tag{$\ 1\ $}\] しかしながら,$\cos$,$\sin$ の周期性から知られる通り\[\theta=\frac{2k\pi}{n},\ \ \ \theta^\prime=\frac{2k^\prime\pi}{n}\]に対応する $n$ 乗根は $\theta-\theta^\prime$ が $2\pi$ の倍数,したがって $k-k^\prime$ が $n$ の倍数,すなわち $k\equiv k^\prime\hphantom{m}\left(\text{mod}.\ n\right)$ であるときに限って相等しいから,$1$ の $n$ 乗根をことごとく得るために $\left(\ 1\ \right)$ において $k$ に与えるべき値は,$n$ を法としての一つの剰余系である.$\left(\ 1\ \right)$ において $\left(k,\ n\right)=1$ のときは,$2k\pi/n$ は $n$ 倍して初めて $2\pi$ の倍数になるから,\[\cos\frac{2k\pi}{n}+i\sin\frac{2k\pi}{n}\]は $n$ 乗して初めて $1$ に等しくなるものである.これらを $1$ の原始 $n$ 乗根という.もしも $\left(k,\ n\right)=d\gt1$ ならば,$n=dn^\prime$,$k=dk^\prime$ と置くとき,\[\frac{2k\pi}{n}=\frac{2k^\prime\pi}{n^\prime}\]であるから,\[\cos\frac{2k\pi}{n}+i\sin\frac{2k\pi}{n}\]は $n^\prime$ 乗してすでに $1$ に等しくなる.すなわち $1$ の $n^\prime$ 乗根である.
〔定理 $\boldsymbol{1.\ 23}$〕 $1$ の原始 $n$ 乗根は $\varphi\left(n\right)$ 個ある.それらは\[\cos\frac{2k\pi}{n}+i\sin\frac{2k\pi}{n}\]において,$k$ に $n$ を法としての既約剰余系の値を与えて得られるものである.
 |
〔定理 $\boldsymbol{1.\ 24}$〕 $n$ の素数分解を $n=p^\alpha q^\beta r^\gamma\cdots\cdots$ とし,\[F_n(x)=\frac{(x^n-1)(x^{\displaystyle\small\frac{n}{pq}}-1)(x^{\displaystyle\small\frac{n}{pr}}-1)(x^{\displaystyle\small\frac{n}{qr}}-1)\cdots\cdots}{(x^{\displaystyle\small\frac{n}{p}}-1)(x^{\displaystyle\small\frac{n}{q}}-1)(x^{\displaystyle\small\frac{n}{r}}-1)\cdots(x^{\displaystyle\small\frac{n}{pqr}}-1)\cdots}\tag{$\ 2\ $}\\[3em]=\overset{d|n}{\textstyle\prod}\ (x^{\displaystyle\small\frac{n}{d}}-1){}^{\mu(d)}\]とすれば,$F_n\left(x\right)$ は $1$ の原始 $n$ 乗根のみを根とする多項式である.
$F_n\left(x\right)$ は $\varphi\left(n\right)$ 次で,その最高項の係数は $1$,その他の係数は皆整数である.$\mu$ は Möbius の函数($48$ 頁)である.
〔証〕 $1$ の原始 $n$ 乗根のみを根(単根)とする方程式を $F_n\left(x\right)=0$ とし,その最高項の係数を $1$ とする.その他の $n$ 乗根は $n$ の或る真の約数 $d$ を次数とする原始 $d$ 乗根で,また $d$ 乗根はもとより全部 $n$ 乗根の中に含まれているから\[\overset{d|n}{\textstyle\prod}F_d\left(x\right)=x^n-1.\] よって定理 $1.\ 22$ における $F\left(n\right)$ と $G\left(n\right)$ とにそれぞれ $F_n\left(x\right)$ と $x^n-1$ とをあて,また和の代わりに積をとり,したがって $u\left(n/d\right)$ を係数とする代わりに,それを指数とするならば\[F_n\left(x\right)=\overset{d|n}{\textstyle\prod}\ (x^{\displaystyle\small\frac{n}{d}}-1){}^{\mu\left(d\right)}\]を得る.これを書き直せば $\left(\ 2\ \right)$ を得る.
$\log$ を用いるならば\[\overset{d|n}{\textstyle\sum}\log F_d\left(x\right)=\log\ (x^n-1)\]から定理 $1.\ 22$ によって\[\log F_n\left(x\right)=\overset{d|n}{\textstyle\sum}\mu\left(d\right)\log\ (x^{\displaystyle\small\frac{n}{d}}-1).\]したがって\[F_n\left(x\right)=\overset{d|n}{\textstyle\prod}\ (x^{\displaystyle\small\frac{n}{d}}-1){}^{\mu\left(d\right)}.\]この計算では,$x$ を十分大きい正数として $F_d\left(x\right)$,$x^n-1$ が正の値を有するものとして,$\log$ の実数値をとると考えるがよい.最後の結果はもちろん $x$ に関する恒等式である(代.$\S\ 22$).
$F_n\left(x\right)$ の次数はもちろん $\varphi\left(n\right)$ で,その係数は $\left(\ 2\ \right)$ から見える通り,整数である:$\left(\ 2\ \right)$ の分子と分母とにおける積を展開して後に,割り算を行なうと想像すれば,分母の最高項の係数が $1$ であるから,割り算に際して商の係数に分数の生ずる余地がない.
例えば\[F_{12}\left(x\right)=\frac{\left(x^{12}-1\right)\left(x^2-1\right)}{\left(x^6-1\right)\left(x^4-1\right)}=\frac{x^6+1}{x^2+1}=x^4-x^2+1.\] また $p$ が素数ならば,\[F_p\left(x\right)=x^{p-1}+x^{p-2}+\cdots\cdots+x+1,\\F_{p^{\ e}}\left(x\right)=x^{p^{\ e-1\ }\left(p-1\right)}+x^{p^{\ e-1\ }\left(p-2\right)}+\cdots+x^{p^{\ e-1\ }}+1.\] 〔問題 $\boldsymbol{1}$〕 $F_n\left(x\right)$ の常数項は,$n=1$ の場合のほか,$+1$ である.
〔問題 $\boldsymbol{2}$〕 $F_n\left(x\right)$ の第二項の係数は $-\mu\left(n\right)$ に等しい.すなわち $1$ の原始 $n$ 乗根の和は $\mu\left(n\right)$ に等しい.
〔解〕 原始 $n$ 乗根の和を $f\left(n\right)$ とすれば,$x^n-1=0$ から\[\overset{d|n}{\textstyle\sum}f\left(d\right)=\begin{cases}1,&n=1\ のとき,\\0,&n\gt1\ のとき.\end{cases}\]
| 故に(定理 $1.\ 22$) | $\begin{alignat*}{1}f\left(n\right)&=\mu\left(n\right)\hspace{0.7mm}\cdotp1+\mu\left(d\right)\hspace{0.7mm}\cdotp0+\cdots\cdots+\mu\left(1\right)\hspace{0.7mm}\cdotp0\\&=\mu\left(n\right)\end{alignat*}$ |
〔解〕 $\rho^k$ は無論 $1$ の $n$ 乗根であるが,$\rho$ が原始 $n$ 乗根であるから $\rho$ の巾が $1$ に等しいのは指数が $n$ の倍数であるときに限る.故に $\rho^k=\rho^{k\prime}$ になるのは,$k\equiv k^\prime\hphantom{m}\left(\text{mod}.\ n\right)$ のときに限る.
$k$ に $n$ を法としての完全な代表の一組の値を与えるとき,$\rho^k$ から $n$ 個の相異なる $n$ 乗根,すなわちすべての $n$ 乗根が出てくる.
また $\left(k,\ n\right)=d$,$n=dn^\prime$ とすれば $\left(\rho^k\right){}^{n\prime}=1$.また $\left(\rho^k\right){}^e=1$ ならば,$ke$ は $n$ の倍数,よって $e$ は $n^\prime$ の倍数である.すなわち $\rho^k$ は原始 $n^\prime$ 乗根である.特に $d=1$ のときに,$\rho^k$ は原始 $n$ 乗根である.
〔問題 $\boldsymbol{4}$〕 $\left(a,\ b\right)=1$ ならば,$1$ の $a$ 乗根と $b$ 乗根とをすべての組合せに掛けて得られる $ab$ 個の積が,$1$ の $ab$ 乗根の全部になる.もしも原始 $a$ 乗根と原始 $b$ 乗根とのみを掛け合わせるならば,原始 $ab$ 乗根だけ得られる.
〔解〕 $\alpha=\cos\dfrac{2\pi}{a}+i\sin\dfrac{2\pi}{a}$,$\beta=\cos\dfrac{2\pi}{b}+i\sin\dfrac{2\pi}{b}$ とすれば\[\alpha^x\beta^y=\cos\frac{2\left(bx+ay\right)\pi}{ab}+i\sin\frac{2\left(bx+ay\right)\pi}{ab}.\] ここで $x$,$y$ にそれぞれ $a$,$b$ を法としての剰余系[または既約剰余系]の値を与えるならば,$bx+ay$ は $ab$ を法としての剰余系[または既約剰余系]の値をとる(定理 $1.\ 19$).故に問題にいう通りになる.