第 $2$ 章 連 分 数
$\S\ 24.$ 格 子
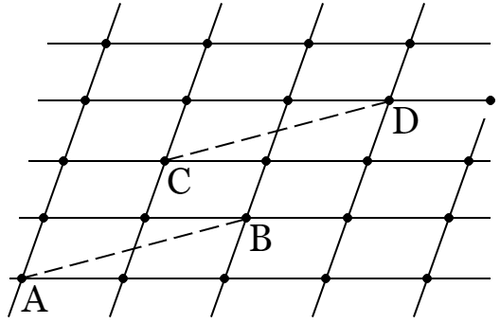
$\boldsymbol{1.}$ 平面上におのおの一定の距離を保って二組の平行線を引けば,平面が互いに合同な無数の平行四辺形でおおわれる.このような図形を格子といい,平行線の相交わる点を格子点という.この図形に平行移動を行なって,一つの格子点を他の一つの格子点の位置に来させるときは,図形は全体として原位置における図形と一致する.換言すれば,$\mathrm{A}$,$\mathrm{B}$,$\mathrm{C}$ を任意の三つの格子点とするとき,$\mathrm{C}$ を起点としてベクトル $\mathrm{AB}$ に等しいベクトル $\mathrm{CD}$ を引けば,その端 $\mathrm{D}$ は,やはり一つの格子点である.これが格子の基本的性質である.
 |
平面上に直交座標をとるときは,整数座標を有する点の全体は一組の格子点である.いま格子点 $\mathrm{A}\left(a,\ b\right)$ と $\mathrm{B}\left(c,\ d\right)$ との座標の間に\[ad-bc=1\tag{$\ 1\ $}\]なる関係があるとすれば,$\mathrm{OA}$,$\mathrm{OB}$ を二辺とする平行四辺形の面積は $1$ に等しい.さて\[\begin{alignat*}{1}x&=au+cv,\\[2mm]y&=bu+dv\end{alignat*}\tag{$\ 2\ $}\]と置けば,$\left(\ 1\ \right)$ を用いて\begin{alignat*}{1}u&=dx-cy,\\[2mm]v&=-bx+ay\end{alignat*}を得る.したがって各格子点 $\mathrm{P}\left(x,\ y\right)$ には $u$,$v$ の整数値が対応し,また $u$,$v$
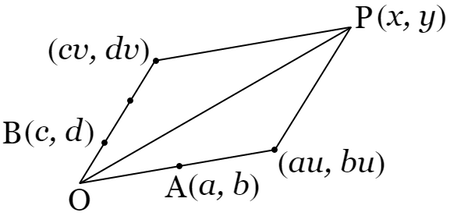 |
さて $\left(\ 2\ \right)$ によって,ベクトル $\overline{\mathrm{OP}}$,$\overline{\mathrm{OA}}$,$\overline{\mathrm{OB}}$ の間に次の関係がある:\[\overline{\mathrm{OP}}=u\hspace{0.7mm}\cdotp\overline{\mathrm{OA}}+v\hspace{0.7mm}\cdotp\overline{\mathrm{OB}}\tag{$\ 3\ $}\]これが点 $\mathrm{P}$ に対応する整数 $\left[u,\ v\right]$ の意味である.
よって $\mathrm{OA}$,$\mathrm{OB}$ を二辺とする平行四辺形を基本として,それと合同な平行四辺形をもって全平面をおおうときは,そのようにして生ずる格子点は全体として原格子点と一致する.
$\left(\ 1\ \right)$ の整数解は無数にあるから,同一の格子が,格子点に関する限り,無数の相異なる平行四辺形から生み出されるのである.
$\mathrm{OA}$ を $u$ 軸,その上の長さは $\mathrm{OA}$ を単位として計り,また $\mathrm{OB}$ を $v$ 軸,その上の長さは $\mathrm{OB}$ を単位として計ることにすれば,$\left[u,\ v\right]$ はすなわちこの座標法に関する点 $\mathrm{P}$ の座標である.
上記では通常の直角座標を用いて正方格子を基本としたのであったが,初めから任意の格子を基本にして,このような一般的の平行座標を用いても同じ結果が得られるのである.
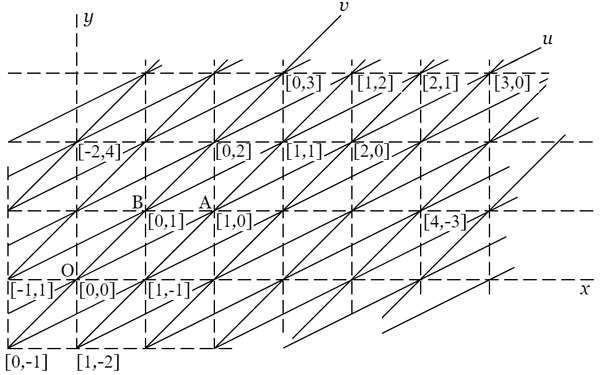 |
実際,この場合には任意の格子点 $\mathrm{P}$ に関して,整数 $u$,$v$ をもって $\left(\ 3\ \right)$ が成り立たなければならない.換言すれば,任意の整数 $x$,$y$ に関して,$\left(\ 2\ \right)$ が整数解 $u$,$v$ を有する.
さて $\left(\ 2\ \right)$ から\[\begin{alignat*}{1}u&=\frac{d}{\varDelta}x-\frac{c}{\varDelta}y\\[2mm]v&=\frac{-b}{\varDelta}x+\frac{a}{\varDelta}y\end{alignat*}\hspace{1cm}\varDelta=ad-bc.\] 故に $x=1$,$y=0$ および $x=0$,$y=1$ に対する $u=d/\varDelta$,$v=-b/\varDelta$ および $u=-c/\varDelta$,$v=a/\varDelta$ は整数であるから\[\frac{d}{\varDelta}\frac{a}{\varDelta}-\frac{b}{\varDelta}\frac{c}{\varDelta}=\frac{1}{\varDelta}\]が整数である.$\varDelta$ は整数であるから $\varDelta=\pm1$.
〔問題 $\boldsymbol{1}$〕 四つの頂点が格子点である平行四辺形 $\mathrm{ABCD}$ において,相接する二辺 $\mathrm{BC}$,$\mathrm{CD}$ の上にある格子点を除いて,内部かつ周上に $N$ 個の格子点があるならば,面積は $N$ に等しい.
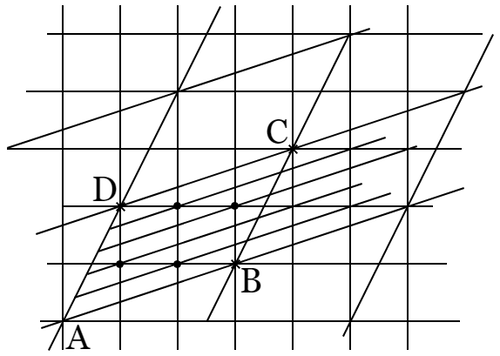 |
もしも $\mathrm{ABCD}$ が四つの頂点のほか,内部にも周上にも格子点を含まないならば,$N=1$($\mathrm{A}$ だけが $\mathrm{ABCD}$ に属する).この場合には $\mathrm{ABCD}$ から生ずる格子点は原格子点と一致して,$\mathrm{ABCD}$ の面積は $1$ に等しいことは前に述べた通りである.問題はそれの拡張である.
〔解〕 辺 $\mathrm{AB}$ または $\mathrm{AD}$ の中途に格子点があるならば,格子点は等距離を置いて分布されるから,それらを通って辺に平行な直線を引いて $\mathrm{ABCD}$ を等分すれば,各平行四辺形に分属する格子点も同数に等分される.故に初めから $\mathrm{ABCD}$ の各辺の中途には格子点はないものと仮定してもよい.
さて $\mathrm{AB}$ に平行な直線をもって原格子点の全部を分載するとき($149$ 頁),これらの平行線のうち $\mathrm{AB}$ と $\mathrm{DC}$ との中間にあるものは,$\mathrm{AD}$,$\mathrm{BC}$ の間においておのおの一つずつの格子点を含むから,これらの平行線の数は $N-1$ で,それらは $\mathrm{ABCD}$ を $N$ 等分するが,その各部分の面積は $1$ に等しい.故に $\mathrm{ABCD}$ の面積は $N$ に等しい.
$\boldsymbol{2.}$ 連分数の理論は格子を用いて幾何学的に考察すれば,最も明瞭である.
いま $\omega$ を無理数として,$y=\omega x$ なる直線(略して $\omega$ 線という)を引けば,この直線は原点のほか一つも格子点を通過しない($\omega$ 線が格子点 $\left(x,\ y\right)$ を通るならば $\omega=y/x$ は有理数でなければならない).故に $\mathrm{O}$ 以外の格子点は $\omega$ 線によって両分される.もしも格子点 $\left(x,\ y\right)$ に有理数 $y/x$ を対応させるならば,すべての有理数,特に $\omega$ の主,または中間近似分数に対応する格子点は,その有理数と $\omega$ との大小の関係に従って,$\omega$ 線の上側または下側に配置される.
いま明確のために $n$ を偶数として,近似分数 $p_{n-1}/q_{n-1}$,$p_n/q_n$ に対応する格子点 $\mathrm{A}\left(q_{n-1},\ p_{n-1}\right)$,$\mathrm{B}\left(q_n,\ p_n\right)$ を $\omega$ 線の両側に記し,平行四辺形 $\mathrm{OAA}^\prime\mathrm{B}$ を基本として格子を作れば,$p_nq_{n-1}-p_{n-1}q_n=1$ であるから,その格子点は,全体において,原格子点と一致する.特に $\mathrm{AA}^\prime$ の延長上にある格子点を $\mathrm{A}^{\prime\prime}$,$\cdots\cdots$,$\mathrm{C}$,$\mathrm{B}^\prime$ として,$\mathrm{CB}^\prime$ が $\mathrm{L}$ において $\omega$ 線に交わるとすれば,\[\mathrm{OB}=\mathrm{AA}^\prime=\mathrm{A}^\prime\mathrm{A}^{\prime\prime}=\cdots\cdots=\mathrm{CB}^\prime.\] $\mathrm{AA}^\prime$ は $\mathrm{OB}$ に平行であるから,$\mathrm{AA}^\prime$ の延長上の点の座標を\[q_{n-1}+tq_n,\ \ p_{n-1}+tp_n\]とすることができる.$t$ の整数値 $1$,$2$,$\cdots\cdots$ に対応する点はすなわち格子点 $\mathrm{A}^\prime$,$\mathrm{A}^{\prime\prime}$,$\cdots\cdots$ で,また $\omega$ 線との交点 $\mathrm{L}$ に関しては
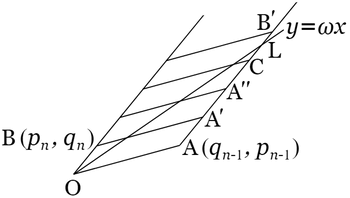 |
よって $\mathrm{AA}^\prime$ の延長上において,$\omega$ 線の下側にある最後の格子点 $\mathrm{C}$ に関しては $t=k_n$,すなわち $\mathrm{C}$ の座標は $q_{n-1}+k_nq_n=q_{n+1}$,$p_{n-1}+k_np_n=p_{n+1}$で,$\mathrm{C}$ は主なる近似分数 $p_{n+1}+q_{n+1}$ に対応する.
また $t=1$,$2$,$\cdots\lt k_n$ に対応する $\mathrm{A}^\prime$,$\mathrm{A}^{\prime\prime}$,$\cdots$ は $p_{n-1}/q_{n-1}$ と $p_{n+1}/q_{n+1}$ との間にある中間近似分数に対応する.
$\mathrm{AA}^\prime$ の延長上において $\omega$ 線の上側にある最初の格子点 $\mathrm{B}^\prime$ の座標は $q_{n+1}+q_n$,$p_{n+1}+p_n$ である.したがって $\mathrm{B}^\prime$ は $\omega$ よりも大きい側において $p_n/q_n$ に次ぐ主または中間近似分数 $\left(p_n+p_{n+1}\right)/\left(q_n+q_{n+1}\right)$ に対応する.
主なる近似分数 $p_{n+1}/q_{n+1}$ に対応する格子点 $\mathrm{C}$ が得られた上は,同様の作図によって $\omega$ 線の上側において $p_n/q_n$ に次ぐ近似分数を求めることができる.その最初のものは上記 $\mathrm{B}^\prime$ であるが,$\mathrm{BB}^\prime$ の延長が $\omega$ 線に交わる点を $\mathrm{M}$ とすれば $\mathrm{B}^\prime$ は $\mathrm{B}$ よりも $\omega$ 線に近いから $\mathrm{M}$ は $\mathrm{B}^\prime$ よりも右にある. $\mathrm{BM}$ の上には格子点は $\mathrm{BB}^\prime=\mathrm{OC}$ に等しい距離をもつて配置される.それらの格子点の中で $\omega$ 線の上側にある最後のものは主なる近似分数 $p_{n+2}/q_{n+2}$ に対応し,$\omega$ 線の下側にある最初のものは $\omega$ よりも小で,$p_{n+1}/q_{n+1}$ に次ぐ最初の主または中間近似分数に対応する(上の図は誇張して描いてある).
このようにして $\omega$ 線の両側において,近似分数に対応する格子点のみを通る二つの折線が得られ,折線の折れ目(頂点)は主なる近似分数に対応し,各辺の中途にある格子点は中間近似分数に対応する.
これらの折線を作図するには $x$ 軸および $y$ 軸上に格子点 $\mathrm{A}_{-1}\left(1,\ 0\right)$ および $\mathrm{A}_0\left(0,\ 1\right)$ をとって,それを起点とするがよい.
 |
$\mathrm{A}_{-1}$,$\mathrm{A}_0$,$\mathrm{A}_1$,$\mathrm{A}_0{}^\prime$ は $151$ 頁の作図における $\mathrm{A}$,$\mathrm{B}$,$\mathrm{C}$,$\mathrm{B}^\prime$ に該当する.
$p_1/q_1$,$p_2/q_2$ に対応する $\mathrm{A}_1$,$\mathrm{A}_2$ が得られた上は$151$ 頁に示した方法によって,つぎつぎに $p_3/q_3$,$p_4/q_4$,$\cdots\cdots$ に対応する $\mathrm{A}_3$,$\mathrm{A}_4$,$\cdots\cdots$ を求めていくことができる.
このようにして $\omega$ 線の両側に生ずる折線 $\mathrm{A}_{-1}\mathrm{A}_1\mathrm{A}_3\mathrm{A}_5\cdots\cdots$,$\mathrm{A}_0\mathrm{A}_2\mathrm{A}_4\cdots\cdots$ の中間には格子点が一つも含まれないことは明白である.
$151$ 頁の図から見えるように,三角形 $\mathrm{OAL}$ の内部には格子点はない.したがって $\mathrm{A}$,$\mathrm{C}$(すなわち $\mathrm{A}_{n-1}$,$\mathrm{A}_{n+1}$ を通る縦線と $\omega$ 線および $\mathrm{AC}$ とで囲まれた四角形の内部に格子点はあり得ないのである.
各折線上において格子点は右の方へ進むにしたがって,いよいよ $\omega$ 線に近くなることは,作図によって明白である.これらの格子点の特徴は,$\omega$ 線の同じ側で,それ自身よりも左にあるどの格子点よりも $\omega$ 線に近いことである.
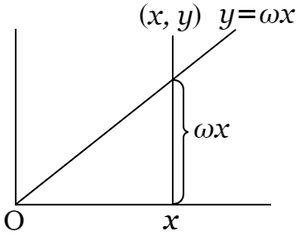 |
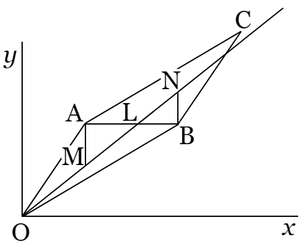
定理 $2.\ 8$ の第一の部分をも証明するには,二つの折線上の格子点を一緒にして,$\omega$ 線への距離を比較しなければならない.$151$ 頁の図に返っていえば $\mathrm{A}$,$\mathrm{A}^\prime$,$\mathrm{A}^{\prime\prime}$,$\cdots\cdots$,$\mathrm{C}$ と反対側の $\mathrm{B}$ とからの距離の大小が問題であるが,$\omega$ 線への垂直距離,または上記 $\left|y-\omega x\right|$ の代わりに,$\mathrm{OB}$ に平行に $\omega$ 線に至る距離をとってもよい.しからば図を一見して明らかな通り,\[\mathrm{AL}\gt\mathrm{A}^\prime\mathrm{L}\gt\mathrm{A}^{\prime\prime}\mathrm{L}\gt\cdots\cdots\gt\mathrm{OB}\]で,$\mathrm{C}$ に至って初めて $\mathrm{CL}\lt\mathrm{OB}$ になる.
すなわち $\mathrm{B}\left(q_n,\ p_n\right)$ よりも右にある格子点 $\left(x,\ y\right)$ の中で,初めて\[\left|p_n-q_n\omega\right|\gt\left|y-\omega x\right|\]になるものは,$\mathrm{C}\left(q_{n+1},\ p_{n+1}\right)$ であって,中間近似分数に対応する $\mathrm{A}^\prime$,$\mathrm{A}^{\prime\prime}$,$\cdots\cdots$ には,その資格がないのである.
〔問題 $\boldsymbol{2}$〕 $\omega$ は無理数,$a/b$,$c/d$ は有理数で\[\frac{a}{b}\gt\omega\gt\frac{c}{d},\hspace{5mm}ad-bc=1\]ならば,$a/b$ も $c/d$ も近似分数で,しかも少なくとも一方は主なる近似分数である.
〔解〕 近似分数であることは 定理 $2.\ 6$ から直ぐにわかる.$a/b\gt y/x\gt\omega$ ならば $a/b\gt y/x\gt c/d$ から $x\geqq b+d$,故に $a/b$ は優良近似値,したがって近似分数である.$c/d$ も同様,
さて $b\gt0$,$d\gt0$ と仮定して\begin{alignat*}{1}x&=bu+dv,\\[2mm]y&=au+cv\end{alignat*}と置けば,仮定によって $x$,$y$ の整数値と $u$,$v$ の整数値とは互いに対応する.いま $0\lt x\lt b+d$ とすれば,$u=0$,$v\gt0$;$u\gt0$,$v=0$,または $uv\lt0$.故に $\left|y-\omega x\right|=\left|v\left(c-d\omega\right)\ \!\right|$,または $\left|y-\omega x\right|=\left|u\left(a-b\omega\right)\ \!\right|$ または $a-b\omega$,$c-d\omega$ は反対の符号を有するから,$uv\lt0$ のとき\[\left|y-\omega x\right|=\left|u\left(a-b\omega\right)\ \!\right|+\left|v\left(c-d\omega\right)\ \!\right|.\]すなわち $x$ を上記の限界内に限るとき $\left|y-\omega x\right|$ の最小値は $\left|a-b\omega\right|$ または $\left|c-d\omega\right|$ である.故に\[a-b\omega\lessgtr d\omega-c,\ \ すなわち \omega\gtrless\frac{a+c}{b+d}\]にしたがって $a/b$ または $c/d$ が主なる近似分数である(定理 $2.\ 8$ 〔第一〕).
この問題も幾何学的に考察すれば明白である.
 |
〔問題 $\boldsymbol{3}$〕 $\omega$ は無理数,$p/q$ は有理数で,
 |
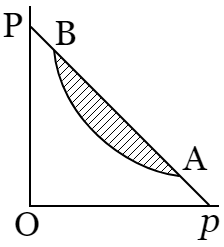
〔解〕 $\mathrm{A}$ を点 $\left(q,\ p\right)$ とし,$\mathrm{A}$ から $\omega$ 線への平行線を $\mathrm{AC}$,また $\omega$ 線の反対の側においてそれと等距離にある平行線を $\mathrm{BD}$ とする.ただし $\mathrm{AB}$ は $y$ 軸に平行である.上記の関係は $\left|q\left(q\omega-p\right)\ \!\right|\lt1/2$ で,この左辺は平行四辺形 $\mathrm{OPAC}$ の面積である($底\ \mathrm{AP}=\left|q\omega-p\right|$,$高=q$).故に $\mathrm{ABDC}$ の面積は $1$ よりも小である.したがって $\mathrm{ABDC}$ の内部には格子点がない.なぜならば,もし内部に格子点 $\mathrm{U}$ があるとすれば,三角形 $\mathrm{OAU}$ は格子点を頂点とするから,その面積は少なくとも $1/2$ である.$\mathrm{OAU}$ は平行四辺形 $\mathrm{ABDC}$ の半分以下だから,これは矛盾である.$\mathrm{ABDC}$ の内部に格子点がないから,定理 $2.\ 8$〔第一〕によって $p/q$ は主なる近似分数である.
上記では $p/q$ を既約分数と仮定した(故に $\mathrm{U}$ は $\mathrm{OA}$ 上にはない).既約でなければ,約分して $p^\prime/q^\prime$ とすれば,$\left|q^\prime\left(q^\prime\omega-p^\prime\right)\ \!\right|\lt1/2$ を得る.
〔注意〕 $\left|\ \!\omega-\left(p/q\right)\ \!\right|\lt1/q^2$ でも,$p/q$ は主,または中間近似分数である.
上記と同じ記号を用いるならば,この場合平行四辺形 $\mathrm{OPAC}$ の面積は $1$ よりも小である.よってその内部または周上に格子点を含み得ない.故に定理 $2.\ 8$〔第二〕によって $p/q$ は主,または中間近似分数である(ここでも,もちろん $p/q$ は既約分数と見てよい).
〔問題 $\boldsymbol{4}$〕 二つの相接する主なる近似分数のうち,少なくとも一方は問題 $3$ の条件を満たす(Vahlen の定理).
 |
| 〔解〕 | $\left|\ \!\omega-\dfrac{p_n}{q_n}\right|=\dfrac{1}{q_n\left(q_n\omega_n+q_{n-1}\right)}=\dfrac{1}{\rho_nq_n{}^2}$ |
さて $x$,$y$ が正で\[x+y\leqq\rho,\hspace{1cm}\frac{1}{x}+\frac{1}{y}\leqq\rho\]ならば,$\rho\geqq2$ で,$x$,$y$,$1/x$,$1/y$ は\[\frac{\rho+\sqrt{\rho^2-4}}{2} と \frac{\rho-\sqrt{\rho^2-4}}{2}\]との中間にあることは見やすい.
 |
故に $\rho_{n-1}=\dfrac{1}{\omega_n}+\dfrac{q_n}{q_{n-1}}\leqq\rho$,$\rho_n=\omega_n+\dfrac{q_{n-1}}{q_n}=\dfrac{1}{\omega_{n+1}}+\dfrac{q_{n+1}}{q_n}\leqq\rho$,$\rho_{n+1}=\omega_{n+1}+\dfrac{q_n}{q_{n+1}}\leqq\rho$ ならば,$\dfrac{q_{n-1}}{q_n}$ も $\dfrac{q_{n+1}}{q_n}$ も上記の区間に属するから\[k_n=\frac{q_{n+1}}{q_n}-\dfrac{q_{n-1}}{q_n}\leqq\frac{\rho+\sqrt{\rho^2-4}}{2}-\frac{\rho-\sqrt{\rho^2-4}}{2}=\sqrt{\rho^2-4}=k_n.\]したがって $\dfrac{q_{n+1}}{q_n}=\dfrac{\rho+\sqrt{\rho^2-4}}{2}=\dfrac{k_n+\sqrt{k_n{}^2+4}}{2}$ でなければならないが,$\sqrt{k^2{}_n+4}$ は($k_n\gt0$)明らかに無理数であるから,これは不合理である.
〔注意〕 $k_n\geqq1$.故に三つの連続する主なる近似分数の中に\[\left|\ \!\omega-\frac{p}{q}\right|\lt\frac{1}{\sqrt{5}\hspace{0.7mm}\cdotp q^2}\]なるものが必ずある.したがって $\omega$ が無理数ならば,このような分数 $p/q$ が無数にある.また $k_n$ がついに $1$ になってしまう(終項が $1+\dfrac{1}{1}\raise{0.2em}{\underset{\Large+}{}}\dfrac{1}{1}\raise{0.2em}{\underset{\Large+}{}}\ \underset{\Large\cdots}{}\ \underset{\Large\cdots}{}\ =\dfrac{\sqrt{5}+1}{2}$ になる)場合を除けば $k_n\geqq2$ なるものが無数にあるから\[\left|\ \!\omega-\frac{p}{q}\right|\lt\frac{1}{\sqrt{8}\hspace{0.7mm}\cdotp q^2}\]なる分数 $p/q$ が無数にある(Hurwitz および Borel の定理).