第 $2$ 章 連 分 数
$\S\ 26.$ Minkowski の定理
$\boldsymbol{1.}$ Minkowski は幾何学的の考察を整数論の問題に適用して,いわゆる「数の幾何学」(Geometrie der Zahlen)という分野を開拓した.いまその一班を示すために「一次形式の定理」を紹介する.それは任意数の整変数の一次形式に関するものであるが,ここでは二つの変数の場合について説明する.〔定理 $\boldsymbol{2.\ 10}$〕 $\alpha$,$\beta$,$\gamma$,$\delta$ は実数,$\varDelta=\alpha\delta-\beta\gamma\neq0$,また $h$,$k$ は正数で,$hk=\left|\varDelta\right|$ とする.しからば\[\begin{alignat*}{3}&|\alpha x&&+\beta y&\ \!&|\leqq h\\[2mm]&|\gamma x&&+\delta y&&|\leqq k\end{alignat*}\tag{$\ 1\ $}\]は $x=y=0$ 以外の整数解を有する.
〔注意〕 $\alpha=\omega$,$\beta=-1$,$\gamma=1$,$\delta=0$ とすれば $\varDelta=1$.よって $h=1/n$,$k=n$ とすれば $\left(\ 1\ \right)$ は $\left|\ \!\omega x-y\right|\leqq1/n$,$\left|x\right|\leqq n$ になるから,上記の定理を定理 $2.\ 9$ の拡張と見なすことができる.
$\left(\ 1\ \right)$ の両辺を $h$,$k$ で割って\[\alpha^\prime=\frac{\lower{0.1em}\alpha}{\raise{0.1em}h},\hspace{7mm}\beta^\prime=\frac{\lower{0.1em}\beta}{\raise{0.1em}h},\hspace{7mm}\gamma^\prime=\frac{\lower{0.1em}\gamma}{\raise{0.1em}k},\hspace{7mm}\delta^\prime=\frac{\lower{0.1em}\delta}{\raise{0.1em}k}\]と置けば $\alpha^\prime\delta^\prime-\beta^\prime\gamma^\prime=1$ で,$\left(\ 1\ \right)$ は\begin{alignat*}{3}&|\alpha^\prime x&&+\beta^\prime y&&|\leqq1\\[2mm]&|\gamma^\prime x&&+\delta^\prime y&&|\leqq1\end{alignat*}になるから定理を $\varDelta=1$,$h=k=1$ なる場合に証明すれば十分である.
〔証〕 まず $\alpha$,$\beta$($\gamma$,$\delta$)が有理数である場合を考察する.この場合には,定理を次のように定理 $2.\ 9$ から導くことができる.
$\alpha$,$\beta$ の分母の公倍数と分子の公約数とをくくり出して\[\alpha x+\beta y=\frac{1}{\nu}\left(ax+by\right)\tag{$\ 2\ $}\]と置いて,$a$,$b$ を互いに素な整数とする.$\nu$ は有理数である.
さて $aq-bp=1$ なる整数 $p$,$q$ を求めて\[\begin{alignat*}{1}X&=ax+by\\[2mm]Y&=px+qy\end{alignat*}\tag{$\ 3\ $}\]とおけば,\[\begin{alignat*}{2}x&=&&qX-bY\\[2mm]y&=-&&pX+aY.\end{alignat*}\tag{$\ 4\ $}\]したがって\[\gamma x+\delta y=\left(\gamma q-\delta p\right)X+\left(-b\gamma+a\delta\right)Y.\]さて $\left(\ 2\ \right)$ から\[-b\gamma+a\delta=\nu\left(-\beta\gamma+\alpha\delta\right)=\nu.\]故に\[\frac{1}{\nu}\left(\gamma q-\delta p\right)=-\omega\]とおけば\[\gamma x+\delta y=\nu\left(-\omega X+Y\right).\]故に問題は\[\begin{alignat*}{1}&\left|X\right|\leqq\nu\\[2mm]&\left|\ \!\omega X-Y\right|\leqq\dfrac{1}{\nu}\end{alignat*}\tag{$\ 5\ $}\]になる.
$x$,$y$ の整数値と,$X$,$Y$ の整数値とは互いに対応するから,$\left(\ 5\ \right)$ に整数解($0$,$0$ 以外)があることを示せばよいのであるが,それは既知である(定理 $2.\ 9,\ 1$)
上記の通り,$\alpha$,$\beta$ が有理数である場合には,定理は証明されたのであるから,それを根拠として,連続性の考察法によって,任意の実係数の場合における証明をする.
$\alpha_n$,$\beta_n$,$\gamma_n$,$\delta_n$($n=1$,$2$,$\cdots\cdots\ \rightarrow\infty$)は有理数で\[\alpha_n\rightarrow\alpha,\ \ \beta_n\rightarrow\beta,\ \ \gamma_n\rightarrow\gamma,\ \ \delta_n\rightarrow\delta,\ \ \alpha_n\delta_n-\beta_n\gamma_n=1\tag{$\ 6\ $}\]とする.しからば\[\begin{alignat*}{1}\xi_n&=\alpha_nx_n+\beta_ny_n\\[2mm]\eta_n&=\gamma_nx_n+\delta_ny_n\end{alignat*}\tag{$\ 7\ $}\]とおくとき\[\begin{alignat*}{1}\left|\xi_n\right|&\leqq1\\[2mm]\left|\eta_n\right|&\leqq1\end{alignat*}\tag{$\ 8\ $}\]は $\left\{0,\ 0\right\}$ 以外の整数解 $\left\{x_n,\ y_n\right\}$ を有することはすでに証明されてあるが,$\left(\ 7\ \right)$ から\begin{alignat*}{3}x_n&=&&\delta_n\xi_n&&-\beta_n\eta_n,\\[2mm]y_n&=-&&\gamma_n\xi_n&&+\alpha_n\eta_n.\end{alignat*}したがって\[\left|x_n\right|\leqq\left|\beta_n\right|+\left|\delta_n\right|,\hphantom{m}\left|y_n\right|\leqq\left|\alpha_n\right|+\left|\gamma_n\right|.\] 故に $\left(\ 6\ \right)$ によって\[\left|\beta_n\right|+\left|\delta_n\right|\lt m,\hphantom{m}\left|\alpha_n\right|+\left|\gamma_n\right|\lt m\]なる一定の数 $m$ をとることができるから,$\left\{x_n,\ y_n\right\}$ なる整数の組合せは有限個数に限る.故に $n=1$,$2$,$\cdots\cdots\rightarrow\infty$ に対応する $\left(\ 8\ \right)$ の整数解の中に,或る同一の整数の組合せ $\left\{x_0,\ y_0\right\}$ が限りなく出てこなければならない(部屋割り論法).
いま $\left(\ 8\ \right)$ の中で $\left\{x_0,\ y_0\right\}$ によって満足させられる無数の $n$ に対応するものだけを残して,その他を除いてしまったとしても,$\left(\ 6\ \right)$ は成り立つ.しからば,それらの $n$ に関して\begin{alignat*}{2}&\left|\alpha_nx_0+\beta_ny_0\right|&&\leqq1,\hspace{1cm}\alpha_nx_0+\beta_ny_0\rightarrow\alpha x_0+\beta y_0,\\[2mm]&\left|\gamma_nx_0+\delta_ny_0\right|&&\leqq1,\hspace{1cm}\gamma_nx_0+\delta_ny_0\rightarrow\gamma x_0+\delta y_0.\end{alignat*}故に\[\left.\begin{alignat*}{3}&|\alpha x_0&&+\beta y_0&&|\leqq1\\[2mm]&|\gamma x_0&&+\delta y_0&&|\leqq1\end{alignat*}\right\}\]すなわち定理が証明されたのである.
$\boldsymbol{2.}$ 上記の定理 $2.\ 10$ は,それを幾何学的にいい表わすとき,その意味が鮮明に了解される.
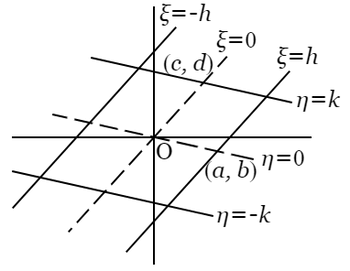
平面上に直角座標をとって正方格子を作り,$\left(\ 1\ \right)$ における $x$,$y$ をその格子点の座標とする.
さて一般に\[-h\leqq\alpha x+\beta y\leqq h\]なる点 $\left(x,\ y\right)$ は方程式\[\alpha x+\beta y=\pm h\tag{$\ 9\ $}\]によって表わされる二つの平行線の中間を出ない.同様に\[-k\leqq\gamma x+\delta y\leqq k\]なる点 $\left(x,\ y\right)$ は\[\gamma x+\delta y=\pm k\tag{$10$}\]なる二つの平行線の中間を出ない.故に $\left(\ 1\ \right)$ を満足させる整数 $x$,$y$ は $\left(\ 9\ \right)$,$\left(10\right)$ の二対の平行線によってかこまれた平行四辺形の内部または周上にある格子点の座標である.
しかるに\[hk=\left|\alpha\delta-\beta\gamma\right|\]なる関係は,この平行四辺形の面積が $4$ に等しいことを示すものである.
 |
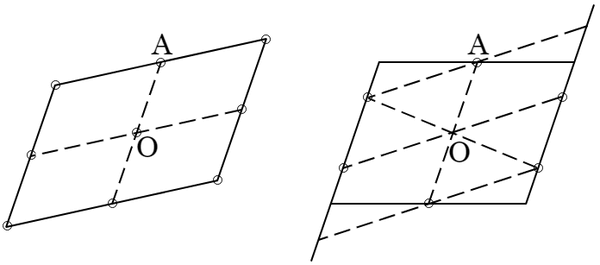
〔定理 $\boldsymbol{2.\ 10,\ 1}$〕 面積 $1$ なる正方形を基本とする格子の一点に中心を置いて,面積 $4$ なる任意の平行四辺形を描けば,その内部または周上に中心以外の格子点が必ず含まれる.
平行四辺形の面積を $4$ とすれば,上記定理において「または周上」の一句が必要である.例えば格子の基本をなす平行四辺形を四個連結して作られる平行四辺形をとれば,中心以外の格子点は周上にのみあって,内部にはない.しかしもしも面積を $4$ よりも大とすれば,中心以外の格子点が必ず内部に含まれる(面積が $4$ なる平行四辺形を相似的に拡大すれば,周上の格子点が内部に入るから).
座標の原点 $\mathrm{O}$ を中心とする面積 $4$ の平行四辺形がその内部に $\mathrm{O}$ 以外の格子点を含む場合には,定理 $2.\ 10$ の二つの関係式において,両所ともに不等号 $\lt$ を置いてよい.さて,かような平行四辺形が内部には $\mathrm{O}$ 以外の格子点を含まないで,周上のみ格子点を有するときには,各辺が格子点を含まなければならない.もしも,かりに一対の相対する辺が(両端以外に)格子点を含まないならば,平行四辺形を少し大きくして,面積が $4$ よりも大で,しかも内部に中心以外の格子点を含まない平行四辺形を得ることになって,定理 $2.\ 10$ に矛盾するであろう.
故に定理 $2.\ 10$ の二つの不等式において,一方だけに記号 $\leqq$ を置いて,他方には記号 $\lt$ を置いても定理は成立する.
定理 $2.\ 9$ の場合: $\left|\ \!\omega x-y\right|\leqq1/n$,$\left|x\right|\leqq n$,($\omega$ は無理数)には,$n\gt1$ とすれば,辺 $\omega x-y=\pm1/n$ の上には格子点があり得ないから,両所とも $\leqq$ を $\lt$ に代えてよい.
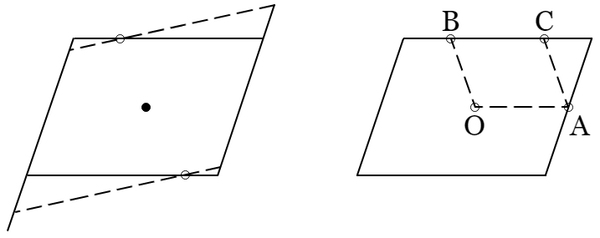
〔問題 $\boldsymbol{1}$〕 面積 $4$ なる平行四辺形が中心と周上にのみ格子点を有するとき,周上の格子点の分布は二つの場合に限る.一つは各辺の中点と四つの頂点と,合わせて八つの格子点が周上にある場合で,また一つは一対の相対する辺の中点と他の一対の相対する辺の上に二つずつと合わせて六つの格子点が周上にある場合である.
 |
 |
〔問題 $\boldsymbol{2}$〕 $\alpha$,$\beta$,$\gamma$,$\delta$ は実数で,$\varDelta=\alpha\delta-\beta\gamma\neq0$ ならば\[\left|\ \!\left(\alpha x+\beta y\right)\left(\gamma x+\delta y\right)\ \!\right|\lt\frac{\left|\varDelta\right|}{2}\tag{$\ 6\ $}\]は無数の整数解を有する.
〔解〕 $\varDelta\gt0$ と仮定する.$\xi=\alpha x+\beta y$,$\eta=\gamma x+\delta y$ とおくとき,$\alpha:\beta$[または $\gamma:\delta$]が有理数ならば,$\xi=0$ [または $\eta=0$]が無数の整数解を有して,それらが $\left(\ 6\ \right)$ を満足せしめるから,この場合を除いて考察をする.$x$,$y$ に関する一次式\[\xi-\eta=\left(\alpha-\gamma\right)x+\left(\beta-\delta\right)y\\[2mm]\xi+\eta=\left(\alpha+\gamma\right)x+\left(\beta+\delta\right)y\]の(係数の)行列式は $\left(\alpha-\gamma\right)\left(\beta+\delta\right)-\left(\alpha+\gamma\right)\left(\beta-\delta\right)=2\varDelta$.故に定理 $2.\ 10$ によって\[\begin{alignat*}{1}\left|\ \!\xi-\eta\ \!\right|\leqq\sqrt{2\varDelta}\\[2mm]\left|\ \!\xi+\eta\ \!\right|\leqq\sqrt{2\varDelta}\end{alignat*}\tag{$\ 7\ $}\]が整数解($0$,$0$ を除く)を有する.しかも二個所の $\leqq$ の中どちらでも一方だけは $\lt$ で置き換えてよいのであるから\[\left|\xi\right|+\left|\eta\right|\lt\sqrt{2\varDelta}\]としてよい.しからば\[4\left|\xi\eta\right|\leqq\left(\ \!\left|\xi\right|+\left|\eta\right|\ \!\right)^2\lt2\varDelta,\]したがって\[\left|\xi\eta\right|\lt\frac{\varDelta}{2}.\]$\left(\ 7\ \right)$ の整数解は有限個に限るから,その中に $\left|\xi\right|$ を最小ならしめるものがある($\xi\neq0$,上掲注意).その最小値を $\xi_0$ として $\mu=\xi_0/\sqrt{2\varDelta}$ と置けば,一次式 $\xi/\mu$,$\mu\eta$ の行列式は $\varDelta$ であるから\[\left|\frac{\xi}{\mu}\right|+\left|\mu\eta\right|\lt\sqrt{2\varDelta}\]に整数解 $\left(x,\ y\right)$ がある.そのとき $\left|\xi/\mu\right|\lt\sqrt{2\varDelta}$,したがって $\left|\xi\right|\lt\left|\xi_0\right|$.故にこの整数解は前に得たものとは違う.これから $\left|\xi\eta\right|\lt\varDelta/2$ の新しい整数解を得る.この方法によって $\left(\ 6\ \right)$ の無数の整数解が得られる.
〔注意〕 $\xi=\omega x-y$,$\eta=x$ とすれば,$\varDelta=1$.故に $\left|\ \!x\left(\omega x-y\right)\ \!\right|\lt1/2$ の無数の整数解がある.$\omega$ が無理数ならば,これはすでに連分数論から得られた結果である($\S\ 24$.問題 $4$).$\omega$ が有理数ならば解は $\omega x-y=0$ から得られるので,問題に興味がない.
 |
すなわち拡張された Minkowski の定理は次の通りである.
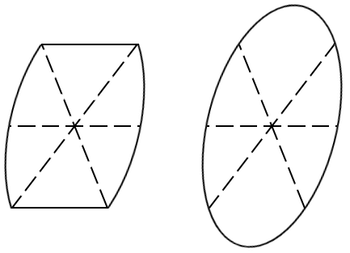
〔定理 $\boldsymbol{2.\ 10,\ 2}$〕 格子点に中心を置いて面積が $\boldsymbol{4}$ なる有心凸形を描けば,その内部または周上に中心以外の格子点が含まれる.
面積 $4$ とは格子の基本である平行四辺形の面積を単位としていうのである.
Minkowski は上記定理をはなはだ独創的な方法で証明したのであるが,ここにそれを述べる余地がない.次に概説する簡単な証明は Birkhoff の着意によるもので,思想上 Dirichlet の証明法に連繋するところに特別の興味がある.
この証明は上記の定理をさらに拡張した次の定理に基づくのである.
〔定理 $\boldsymbol{2.\ 10,\ 3}$〕 格子点の平面上に面積 $s$ なる任意の平面形が置かれてあるとき,それに平行移動を行なって,$s$ よりも多くの格子点を内部または周上に含むような位置に来させることができる.
〔注意〕 平面形が全く無条件ならば,面積 $s$ がいかに大きくても,一つの格子点をも含まないものを描くことはもちろん可能である.そのような平面形でも,もしも平行移動を行なうことを許すならば,必ず $s$ よりも多くの格子点を内部または周上に含むような位置に来させることができるのである.あるいは平行移動を行なわないで,内部または周上に $\left(x_1,\ y_1\right)$,$\left(x_2,\ y_2\right)$,$\cdots\cdots$,$\left(x_n,\ y_n\right)$,$n\gt s$ なる点があって,座標の差 $x_h-x_k$,$y_h-y_k$ がすべて整数に等しいといっても,同じことである.
〔証〕 正方格子の平面上に面積 $s$ なる平面形(それをも $s$ と呼ぶ)が描かれてあるとき,その平面形の内部に着色して,着色された部分を含む各方眼を切りとって,それらを回転しないように一方眼上に重ね合わせたと想像せよ.しからば,それらの方眼の着色部の面積の総和が $s$ であるから,一般には $s$ よりも多くの方眼の着色部が重なっているところがあるであろう(どの点でも着色部の重なっている方眼が $s$ よりも少数ならば,着色部の面積の総和が $s$ よりも小さくなる).いまそのような点に針を立てて各方眼を貫通して後,重ね合わせた方眼をもとの位置に返して,平面形 $s$ の原形を回復したと考えよ.しからば平面形は $s$ よりも多くの針の痕跡を含んでいる.そこで平面形に平行移動を行なって,一つの針の痕を格子点に合わせると,すべての針の痕が格子点に合し,それらが新位置における平面形に含まれるのである.針の痕の座標が上記注意の $\left(x_1,\ y_1\right)$,$\left(x_2,\ y_2\right)$,$\cdots\cdots$,$\left(x_n,\ y_n\right)$ である.
上記の一般的考察において除外されているのは,重ね合わせられた方眼が,どの点においても,ちょうど $s$ 枚ずつ重なり合っている場合である.これは $s$ が整数に等しいときのみ起こり得る極めてきわどい場合である.
この場合には,どの点を針で刺しても,$s$ よりも多くの着色部を貫くことができないから,定理はその言明中「内部または周上」とある一句の「または周上」という抜け道によってのみ救われるのである.それをわかりよくするために,次のような説明を試みる.$s$ の周上の任意の一点 $\mathrm{P}$ を含んで,$s$ の外部に小さいいぼを付けて面積を整数でなくしてしまえば,上記のきわどい事態はたちまち消滅するから,$s$ 枚よりも多くを着色部において貫通する針の立て所が生ずる.その立て所は救いのいぼに属する点でなければならないけれども,いぼはどのように小さくてもよいのだから,$\mathrm{P}$ に針を立ててもよい,$\mathrm{P}$ に針を立てるならば,或る方眼ではその痕が $s$ の境界線上にくるかも知れないが,$s$ の外部に出ることはない.よって,いぼをとり去って,$s$ の原形にかえったとき境界線をも入れて言えば,$s+1$ 以上の針の痕跡がついているのである.
上記の証明では,着意の要点だけを述べたのである.それを技術的証明法の常型に飜訳することは容易でも,話が横道にそれるから,ここで説明することをさしひかえる.
定理 $2.\ 10,\ 3$ から次のようにして Minkowski の定理 $2.\ 10,\ 2$ が得られる.$\mathrm{S}$ は面積 $4$ なる有心凸形で,その中心が格子の原点 $\mathrm{O}$ に置かれてあるとせよ.
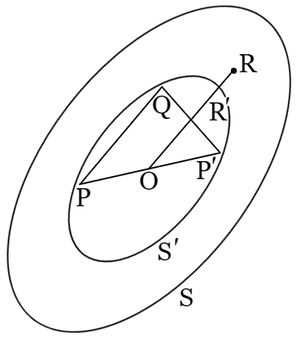 |
このようにして,Minkowski の定理の仮設における面積 $4$,凸形,有心なる三つの要素が定理の終結に寄与する持前が分析されるのである.
〔問題 $\boldsymbol{3}$〕 $a$,$b$,$c$ は実数,$a\gt0$,$D=4ac-b^2\gt0$ ならば\[ax^2+bxy+c^2y\leqq\frac{2\sqrt{D}}{\pi}\]は整数解($0$,$0$ 以外)を有する.
〔解〕 定理 $2.\ 10,\ 2$ の応用,$ax^2+bxy+cy^2=2\sqrt{D}/\pi$ はちょうど面積 $4$ なる楕円である.
〔注意〕実際は上記不等式の右辺で,$\sqrt{D}$ の係数 $2/\pi=0.63\cdots\cdots$ をそれよりも小さい $1/\sqrt{3}=0.57\cdots\cdots$ で置き換えても整数解がある($\S\ 30$,問題 $2$).