第 $2$ 章 連 分 数
$\S\ 30.$ 複 素 数 の 対 等
$\boldsymbol{1.}$ 虚数に関して対等の問題を考察する必要が後に至って生じる.まず任意の複素数\[z=x+yi,\hphantom{m}z_1=x_1+y_1i\]が互いに対等であるために必要な条件を求めるために\[z_1=\frac{pz+q}{rz+s},\hphantom{m}ps-qr=e=\pm1\]と置けば,$z$,$z_1$ と共軛な複素数 $\overline{z}$,$\overline{z}_1$ の間にも\[\overline{z}_1=\frac{p\overline{z}+q}{r\overline{z}+s}\]なる関係が成り立つから,\begin{eqnarray*}z_1-\overline{z}_1&=&\frac{pz+q}{rz+s}-\frac{p\overline{z}+q}{r\overline{z}+s}\\[2mm]&=&\frac{\left(ps-qr\right)\left(z-\right)\overline{z}}{\left|rz+s\right|^2},\end{eqnarray*}すなわち\[y_1=\frac{ey}{\left|rz+s\right|^2}.\tag{$\ 1\ $}\] 故に $e=\pm1$ に従って $y$ と $y_1$ とは同符号または異符号である.すなわち正の「モ変形」は複素数平面の上半部を上半部に変換し,負の「モ変形」は上半部を下半部に変換する(参照 代.$\S\ 6$).
さて $z$,$z_1$ が負の「モ変形」によって結びつけられるときには,$-z$ と $z_1$ とが正の「モ変形」によって結び付けられるから,本節では正の「モ変形」と複素数平面の上半部とのみを考察する.
すなわち $z=x+yi$,$z_1=x_1+y_1i$ において,$y\gt0$,$y_1\gt0$ として,$z$,$z_1$ が正の「モ変形」に関して対等(正式に対等,以下本節では単に対等という)であるか,ないかを決定しようとするのである.
この問題に関して次の基本的の定理が成り立つ.
〔定理 $\boldsymbol{2.\ 13}$〕 複素数平面の上半部にある任意の数は
| $\left(\mathrm{G}\right)$ | \[-\dfrac{1}{2}\leqq x\lt\dfrac{1}{2},\ \ \left|z\right|\geqq1\ \ \left(\left|z\right|=1\hphantom{n}\style{font-family:serif}{\text{ならば,}}\hphantom{n}-\dfrac{1}{2}\leqq x\leqq0\right)\] |
この区域 $\mathrm{G}$ を正の「モ変形」に関する基本区域という(補遺 $9$ 参照).
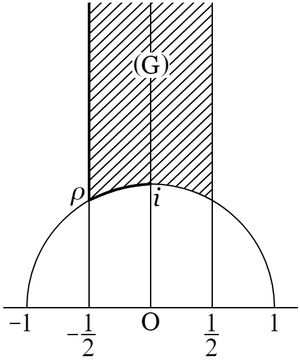 |
$\mathrm{G}$ の底部の境界の左端は $1$ の立方根 $\rho$ で,右端は $6$ 乗根 $-\rho^2$ である.これらは $\mathrm{S}$ によってもまた $\mathrm{T}$ によっても対等である.$\rho+1=-\rho^2$,$-1/\rho=-\rho^2$.また中央の点は $i$ で,それは $\mathrm{T}$ によってそれ自身と対等である.$i=-1/i$.
〔証〕 $z=x+yi$($y\gt0$)を与えられた複素数とし,$z_1=x_1+y_1i$ は $z$ と対等であるとすれば,$\left(\ 1\ \right)$ によって\[y_1=\frac{y}{\left|rz+s\right|^2}.\]故にすべての正の「モ変形」\begin{pmatrix}p&q\\r&s\end{pmatrix}
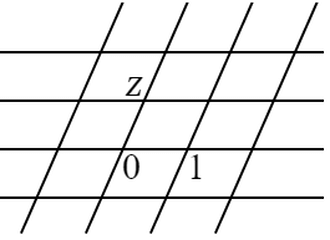 |
このような $z_1$ に関して $a$ を任意の整数とするとき,\[z_1+a\]はやはり $z$ と対等であるから,$a$ を適当に選ぶことによって,その実数部を $-1/2\leqq x\lt 1/2$ なる範囲内に入れることができる.よって $z_1$ の実数部がすでにこの条件を満足すると仮定する.その際\[z_1{}^\prime=\frac{-1}{z_1}\]は $z_1$ と対等,したがって $z$ と対等であるから,$z_1{}^\prime=x_1{}^\prime+y_1{}^\prime i$ とすれば,$\left(\ 1\ \right)$ によって\[y_1{}^\prime=\frac{y_1}{\left|z_1\right|^2}.\]しかるに上記仮定によって\[y_1{}^\prime\leqq y_1,\]故に\[\left|z_1\right|\geqq1,\]したがって $z_1$($\left|z_1\right|=1$ のときは $z_1$ または $z_1{}^\prime$)は区域 $\mathrm{G}$ に属する.すなわち $z$ と対等な数が $\mathrm{G}$ に属することが証明された.
次に定理の後半部を証明するために\[z=x+yi,\hphantom{m}z_1=x_1+y_1i,\hphantom{m}\left(y_1\geqq y\right)\]がともに $\mathrm{G}$ に属するとき,それらは $z_1\neq z$ なる限り,対等であり得ないことを示さなければならない.かりに $z_1$ と $z$ とが対等で,\[z_1=\frac{pz+q}{rz+s}\tag{$\ 2\ $}\]とする.しからば仮定($y_1\geqq y$)によって,$\left(\ 1\ \right)$ から\[\left|rz+s\right|\leqq1.\tag{$\ 3\ $}\]$rz+s$ の虚数部は $ry$ であるから\[\left|ry\right|\leqq1.\]しかるに $z$ は $\mathrm{G}$ に属するから\[y\geqq\frac{\sqrt{3}}{2}.\]故に\[\frac{\sqrt{3}}{2}\left|r\right|\leqq1.\]したがって\[\left|r\right|\leqq\frac{2}{\sqrt{3}},\]$r$ は整数であるから\[r=0 または \pm1.\]$r=0$ とすれば,$ps-qr=1$ から,$p=s=\pm1$.故に $\left(\ 2\ \right)$ から\[z_1=z\pm q.\]$z$ も $z_1$ も $\mathrm{G}$ に属するから,$q=0$.したがって $z_1=z$.
$r=-1$ とすれば,$p$,$q$,$r$,$s$ の符号を変えて $r=1$ とすることができる.よって $r=1$ のみを考察する.しからば $\left(\ 3\ \right)$ から\[\left|z+s\right|\leqq1.\]しかるに $z$ は $\mathrm{G}$ に属し,$s$ は整数であるから,\[s=0,\hspace{1cm}\left|z\right|=1,\]または\[s=1,\hspace{1cm}z=\rho=\frac{-1+\sqrt{-3}}{2}\] $s=0$,$\left|z\right|=1$ とすれば,$ps-qr=1$,$r=1$ から $q=-1$,よって $\left(\ 2\ \right)$ から\[z_1=p-\frac{1}{z}.\]また $z$ は $\mathrm{G}$ に属し,かつ $\left|z\right|=1$ であるから,$z$ は $\mathrm{G}$ の底部の円弧の左半部に属し,したがって $-1/z$ はその右半部に属する.また $z_1$ も $\mathrm{G}$ に属するから,$p=0$,$-1/z=i$,したがって $z_1=i$,$z=i$,すなわち $z_1=z$,または $p=-1$,$-1/z=\left(1+\sqrt{-3}\right)/2=-\rho^2$,したがって $z=\rho$,$z_1=-1-\rho^2=\rho$,すなわち $z_1=z$.
最後に $s=1$,$z=\rho$ とすれば,$ps-qr=1$,$r=1$ から $p-q=1$.すなわち $p=q+1$ で,$\left(\ 2\ \right)$ から\[z_1=\frac{\left(q+1\right)\rho+q}{\rho+1}=q+\frac{\rho}{\rho+1}=q-\rho^2\]であるが,$z_1$ は $\mathrm{G}$ に属するから,$q=-1$,$z_1=\rho$,したがって $z_1=z=\rho$.よって定理の後半部が証明されたのである.
〔問題 $\boldsymbol{1}$〕 $\mathrm{G}$ に属する複素数 $z$ を変えない「モ変形」($z$ の自己変形)は一般には恒等変形以外にない.ただし,$i$ と $\rho$ は例外である.
\begin{eqnarray*}i&=&T\left(i\right),\ \ T=\begin{pmatrix}0&-1\\1&\hphantom{-}0\end{pmatrix}.\\\rho&=&\mathrm{H}\left(\rho\right)=\mathrm{H}^2\left(\rho\right).\hphantom{m}\mathrm{H}=\begin{pmatrix}-1&-1\\\hphantom{-}1&\hphantom{-}0\end{pmatrix},\hphantom{m}\mathrm{H}^2=\begin{pmatrix}\hphantom{-}0&\hphantom{-}1\\-1&-1\end{pmatrix},\hphantom{m}\mathrm{H}^3=\begin{pmatrix}1&0\\0&1\end{pmatrix}.\end{eqnarray*} 〔解〕 上記証明中に示されている.$i=\dfrac{-1}{i}$,$\rho=\dfrac{-\rho-1}{\rho}=\dfrac{1}{-\rho-1}$.
〔問題 $\boldsymbol{2}$〕 正の二次形式 $ax^2+bxy+cy^2$,$a\gt0$,$c\gt0$,$D=4ac-b^2\gt0$($a$,$b$,$c$ は整数でなくてもよい)が $x$,$y$ の整数値($0$,$0$)以外に対してとる最小値は $\sqrt{D/3}$ 以内である.すなわち\[ax^2+bxy+cy^2\leqq\sqrt{\frac{D}{3}}\]は整数解を有する.
等号は $ax^2+bxy+cy^2$ が「モ変形」によって $C\left(X^2+XY+Y^2\right)$ に変換されるときに限って必要である.そのとき $C=\sqrt{D/3}$ ($\S\ 26$,問題 $3$ 参照).
| 〔解〕 | \[ax^2+bcy+cy^2=aN\left(x+\frac{b+i\sqrt{D}}{2a}y\right),\] |
$\boldsymbol{2.}$ 定理 $2.\ 13$ から次の定理が得られる.
〔定理 $\boldsymbol{2.\ 14}$〕 複素数平面の上半部にある二つの複素数 $z$,$z_1$ が対等であるために必要かつ十分な条件は,$z$ および $z_1$ が区域 $\mathrm{G}$ に属する同一の数 $z_0$ と対等であることである.
$z$ と $z_1$ とを $z_0$ に換える「モ変形」を $\mathrm{M}$,$\mathrm{M}_1$ として,\[z_0=\mathrm{M}\left(z\right),\hphantom{m}z_0=\mathrm{M}_1\left(z_1\right)\]とすれば\[z_1=\mathrm{M}_1{}^{-1}\mathrm{M}\left(z\right).\]詳しくいえば,\begin{alignat*}{1}z_0&=\frac{pz+q}{rz+s},&\phantom{m_1}&\mathrm{M}=\begin{pmatrix}p&q\\r&s\end{pmatrix},\\[2mm]z_0&=\frac{p_1z_1+q_1}{r_1z_1+s_1},&\phantom{m_1}&\mathrm{M}_1=\begin{pmatrix}p_1&q_1\\r_1&s_1\end{pmatrix}\end{alignat*}ならば,\[z_1=\frac{p_2z+q_2}{r_2z+s_2}.\]ただし\begin{eqnarray*}&&\begin{pmatrix}p_2&q_2\\r_2&s_2\end{pmatrix}=\begin{pmatrix}p_1&q_1\\r_1&s_1\end{pmatrix}^{-1}\begin{pmatrix}p&q\\r&s\end{pmatrix}=\begin{pmatrix}\hphantom{-}s_1&-q_1\\-r_1&\hphantom{-}p_1\end{pmatrix}\begin{pmatrix}p&q\\r&s\end{pmatrix}\\&=&\begin{pmatrix}\hphantom{-}s_1p-q_1r&\hphantom{-}s_1q-q_1s\\-r_1p+p_1r&-r_1q+p_1s\end{pmatrix}.\end{eqnarray*}よって複素数平面の上半部において $z$ が与えられたとき,$z$ と対等で区域 $\mathrm{G}$ に属する点 $z_0$ を求め,かつ $z$ と $z_0$ とを結び付ける「モ変形」を求める方法が問題になる.
このような「モ変形」は前掲の「モ変形」 $\mathrm{S}$,$\mathrm{T}$ から結合によって組み立てることができる.\[\mathrm{S}=\begin{pmatrix}1&1\\0&1\end{pmatrix},\hphantom{m}\mathrm{S}^{-1}=\begin{pmatrix}1&-1\\0&\hphantom{-}1\end{pmatrix},\hphantom{m}\mathrm{S}^{\pm n}=\begin{pmatrix}1&\pm n\\0&\hphantom{-}1\end{pmatrix}\]であるから,$z$ に $\mathrm{S}^{\pm n}$ なる変形を施すことは,$z$ に $\pm n$ を加えることである.すなわち\[\mathrm{S}^{\pm n}\left(z\right)=z\pm n.\]また\[\mathrm{T}=\begin{pmatrix}0&-1\\1&\hphantom{-}0\end{pmatrix}\]で,$\mathrm{T}=-1/z$($\mathrm{T}^2$ は恒等変形).
さて $z$ の実数部が $-1/2\leqq x\lt1/2$ なる条件を満たしていないならば,正または負の整数 $k$ を適当に定めて,$z_1=\mathrm{S}^k\left(z\right)=z+k$ の実数部を区間 $\left[-1/2,\ 1/2\right)$ に入らせることができる.
そのときもしも $\left|z_1\right|\gt1$ ならば,$z_1$ はすでに $\mathrm{G}$ に属する.もしも $\left|z_1\right|=1$ ならば,$z_1$ の実数部が負または $0$ のとき $z_1$ は $\mathrm{G}$ に属し,それが正のときは,さらに $\mathrm{T}$ を施して,$z_1$ を円弧の左半部に来させる.また,もしも $\left|z_1\right|\lt1$ ならば,$z_1$ に $\mathrm{T}$ を施して,$-1/z_1$ に移れば,その絶対値は $1$ よりも大きくなる.もしもその実数部が区間 $\left[-1/2,\ 1/2\right)$ に属するならば $-1/z_1$ は $\mathrm{G}$ に属する.反対の場合には,さらに $\mathrm{S}^{k_1}$ を施して\[z_2=\mathrm{S}^{k_1}\mathrm{T}\left(z_1\right)\]として,$z_2$ の実数部を $\left[-1/2,\ 1/2\right)$ に入らしめる.そのとき $\left|z_2\right|\gt1$ ならば,$z_2$ は $\mathrm{G}$ に属する.もしも $\left|z_2\right|\leqq1$ ならば,さらに同様の操作を継続する.
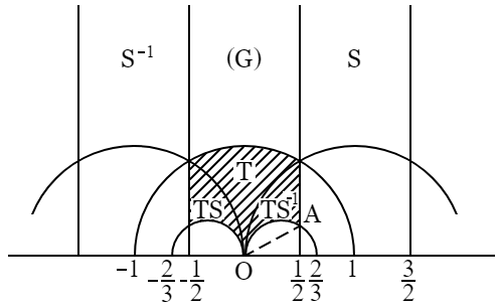
このようにしてつぎつぎに出てくる数の虚数部は次第に増大して,ついには区域 $\mathrm{G}$ に属するものに到達するのである.この論点を明確にするために次の図を描く.図に $\mathrm{S}$,$\mathrm{T}$ 等の文字で示されてある区域は基本区域 $\mathrm{G}$ にそれらの「モ変形」を施すときに生ずる区域である.
この図において,$-1/2$ および $1/2$ を通る縦線の中間で,下方の陰影を付けてない部分に着眼する.この部分に属する点の $\mathrm{O}$ からの距離は $\mathrm{OA}=1/\sqrt{3}$ が最大である.故に $z$ がこの部分にあるとき,それに「モ変形」 $\mathrm{T}$ を施せば,虚数部は $1/\left|z\right|^2$ 倍されるから,$3$ 倍以上になる.故に上記のような操作を反復すれば,ついには $\mathrm{G}$ または陰影の部分に到達せねばならない.さて $\mathrm{T}$ と記した部分に属する点は,それに $\mathrm{T}$ を施せば $\mathrm{G}$ に入る.また $\mathrm{TS}$ または $\mathrm{TS}^{-1}$ なる部分に属する点は,それに $\mathrm{S}^{-1}\mathrm{T}$ または $\mathrm{ST}$ を施せば $\mathrm{G}$ に入る.
 |
これらの「モ変形」を結合して\[\mathrm{S}^{k_n}\mathrm{TS}^{k_{n-1}}\cdots\cdots\mathrm{TS}^k=\begin{pmatrix}p&q\\r&s\end{pmatrix}\]と置けば,\[z_0=\frac{pz+q}{rz+s}\]
| 〔例〕 | $z=\dfrac{39+2i}{61}$. |
| $\mathrm{S}^{-1}\left(z\right)=\dfrac{-22+2i}{61}$,$\mathrm{TS}^{-1}\left(z\right)=\dfrac{11+i}{4}$, | |
| $\mathrm{S}^{-3}\mathrm{TS}^{-1}\left(z\right)=\dfrac{-1+i}{4}$,$\mathrm{TS}^{-3}\mathrm{TS}^{-1}\left(z\right)=2+2i$, | |
| $\mathrm{S}^{-2}\mathrm{TS}^{-3}\mathrm{TS}^{-1}\left(z\right)=2i$,$z_0=2i$ は $\mathrm{G}$ に属する. | |
| $\begin{alignat*}{1}\!\mathrm{S}^{-2}\mathrm{TS}^{-3}\mathrm{TS}^{-1}&=\begin{pmatrix}1&-2\\0&\hphantom{-}1\end{pmatrix}\begin{pmatrix}0&-1\\1&\hphantom{-}0\end{pmatrix}\begin{pmatrix}1&-3\\0&\hphantom{-}1\end{pmatrix}\begin{pmatrix}0&-1\\1&0\end{pmatrix}\begin{pmatrix}1&-1\\0&\hphantom{-}1\end{pmatrix}\\[2mm]&=\begin{pmatrix}-2&-1\\\hphantom{-}1&\hphantom{-}0\end{pmatrix}\begin{pmatrix}-3&-1\\\hphantom{-}1&\hphantom{-}0\end{pmatrix}\begin{pmatrix}1&-1\\0&\hphantom{-}1\end{pmatrix}=\begin{pmatrix}\hphantom{-}5&-3\\-3&\hphantom{-}2\end{pmatrix}.\\[2mm]\therefore\hphantom{\mathrm{TS}^{3}\mathrm{TS}^{-1}}2i&=\frac{5z-3}{-3z+2}.\end{alignat*}$ |
〔解〕 $z$,$z_1$ と対等で $\mathrm{G}$ に属する数を $z_0$ とし,$z_0$ を $z$,$z_1$ に変換する「モ変形」を $\mathrm{U}$, $\mathrm{V}$ とする.すなわち\[z=\mathrm{U}\left(z_0\right),\hphantom{m}z_1=\mathrm{V}\left(z_0\right)\]とする.いま $z_1=\mathrm{M}\left(z\right)$ とすれば\[z_0=\mathrm{V}^{-1}\mathrm{MU}\left(z_0\right).\]$z_0\neq i$,$\neq\rho$ ならば,$z_0$ を変えない「モ変形」($z_0$ の自己変形)は恒等変形 $\mathrm{E}$ に限るから\[\mathrm{V}^{-1}\mathrm{MU}=\mathrm{E},\]したがって\[\mathrm{M}=\mathrm{VU}^{-1}.\]$z_0=i$ ならば,$\mathrm{V}^{-1}\mathrm{MU}=\mathrm{T}$ でもよいから,上記のほかに $\mathrm{M}=\mathrm{VTU}^{-1}$ がある.$z_0=\rho$ ならば $\mathrm{VU}^{-1}$ のほか $\mathrm{VHU}^{-1}$,$\mathrm{VH}^2\mathrm{U}^{-1}$ がある.ただし,$\mathrm{H}=\begin{pmatrix}-1&-1\\\hphantom{-}1&\hphantom{-}0\end{pmatrix}$(問題 $1$).
〔問題 $\boldsymbol{4}$〕 基本区域 $\mathrm{G}$ に「モ変形」 $\mathrm{M}$,$\mathrm{M}^\prime$ を行なうときに生ずる区域には共通の点がない.ただし,境界線上 $i$ および $\rho$ と対等な点だけは例外.
〔解〕 共通の点があるとして,それを $z$ とし,$\mathrm{G}$ において $z$ と対等な点を $z_0$ とすれば,$z=\mathrm{M}\left(z_0\right)=\mathrm{M}^\prime\left(z_0\right)$.故に $z_0=\mathrm{M}^{-1}\mathrm{M}^\prime\left(z_0\right)$.$z_0\neq i$,$\neq\rho$ ならば,これは不可能である.
〔注意〕 $\mathrm{G}$ にすべての「モ変形」を行なって生ずるこれら無数の区域は重複もなく,また隙間もなく,複素数平面の上半部を被うのである.
これらの区域のうち,若干は $190$ 頁の図に示してある.
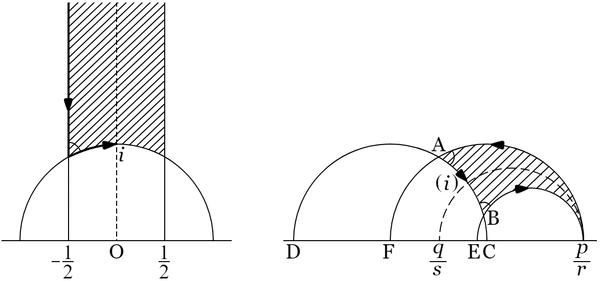
「モ変形」 $\mathrm{M}=\begin{pmatrix}p&q\\r&s\end{pmatrix}$ を $\mathrm{G}$ に行なうときに生ずる区域を $\mathrm{M}$ なる文字で示すならば,$z$ が $\mathrm{G}$ に属すとき,$\mathrm{M}\left(z\right)=\left(pz+q\right)/\left(rz+s\right)$ が区域 $\mathrm{M}$ に属す.
$r=0$ のときには $\mathrm{M}=\mathrm{S}^{\pm q}$ である.区域 $\mathrm{S}^{\pm q}$ は $\mathrm{G}$ を $\pm q$ だけ実数軸に平行に移動させたものである.
$r\neq0$ の場合には,$\mathrm{M}$ は実数軸と直交する円弧で囲まれた弧三角形で,$\mathrm{G}$ の境界の二直線には,$\infty$ に対応する点 $p/r$ において相接する二つの円弧が対応し,$\mathrm{G}$ の底部の境界をなす円弧にはこれらの二つの円と $\pi/3$ の角をなす円弧が対応する.この弧は虚数軸に対応する円(すなわち $\infty$ と $0$ とに対応する $p/r$ と $q/s$ とを直径の両端とする円)と $i$ に対応する $\left(pi+q\right)/\left(ri+s\right)$ において直交する(代.$\S\ 6$).
 |
〔問題 $\boldsymbol{5}$〕 任意の二つの有理数は「モ変形」に関して互いに対等で,それらを結び付ける「モ変形」は無数にある.
〔解〕 二つの有理数を既約分数 $a/c$,$p/r$ として,$ad-bc=1$,$ps-qr=1$ から「モ変形」\[\mathrm{M}=\begin{pmatrix}a&b\\c&d\end{pmatrix},\hphantom{m^\prime}\mathrm{M}^\prime=\begin{pmatrix}p&q\\r&s\end{pmatrix}\]を作れば\[\frac{a}{c}=\mathrm{M}\left(\infty\right),\hphantom{m^\prime}\frac{p}{r}=\mathrm{M}^\prime\left(\infty\right).\]また $\infty$ を $\infty$ に対応せしめる「モ変形」は $\mathrm{S}^n$($n=0$,$\pm1$,$\pm2$,$\cdots\cdots$)である.\[\mathrm{S}^n\left(\infty\right)=\infty.\]故に\[\frac{p}{r}=\mathrm{M}^\prime\mathrm{S}^n\mathrm{M}^{-1}\left(\frac{a}{c}\right).\]すなわち $\mathrm{M}^\prime\mathrm{S}^n\mathrm{M}^{-1}$ が $a/c$ を $p/r$ に変換する「モ変形」の一般の形である.$\mathrm{M}$,$\mathrm{M}^\prime$ は無数にできるが,任意に一つずつきめておくのである.$\mathrm{M}^\prime\mathrm{S}^n=\begin{pmatrix}p&q+np\\r&s+nr\end{pmatrix}$ はすなわち $\mathrm{M}^\prime$ の一般の形であるから,$\mathrm{M}^{-1}$ をきめて $\mathrm{M}^\prime$ は一般にとることにすれば $\mathrm{M}^\prime\mathrm{M}^{-1}$ が求める「モ変形」である.
〔問題 $\boldsymbol{6}$〕 正の「モ変形」 $\mathrm{M}$ を $\mathrm{S}^k$,$\mathrm{T}$ から結合によって作ることができる.すなわち\[\pm\mathrm{M}=\mathrm{S}^{a_0}\mathrm{TS}^{a_1}\mathrm{T}\cdots\cdots\mathrm{S}^{a_{n-1}}\mathrm{TS}^{a_n},\]$a_0$,$a_1$,$\cdots\cdots$,$a_{n-1}$,$a_n$ は正または負の整数で $a_0$ と $a_n$ とは $0$ でもあり得る.
〔解〕 これはすでに上文で述べたことではあるが,実数の範囲内で行列の結合として直接の証明をする.ここでは連分数論を応用するのが適切であろう.
まず\[\mathrm{M}=\begin{pmatrix}a&b\\c&d\end{pmatrix},\hphantom{m^\prime}c\gt d\gt0\]とする.$a/c$ を連分数に展開して\[\frac{a}{c}=k_0+\frac{1}{k_1}\raise{0.2em}{\underset{\Large+}{}}\frac{1}{k_2}\raise{0.2em}{\underset{\Large+}{}}\ \underset{\Large\cdots}{}\ \underset{\Large\cdots}{}\ \raise{0.2em}{\underset{\Large+}{}}\frac{1}{k_{n-1}}\]とする.ただし $n$ を偶数とする(定理 $2.\ 3$).いま
| $\hphantom{_1}z=k_0-\dfrac{1}{z_1}$ すなわち | $\hphantom{_1}z=\mathrm{S}^{k_0}\mathrm{T}\left(z_1\right),$ |
| $z_1=-k_1-\dfrac{1}{z_2}$ | $z_1=\mathrm{S}^{-k_1}\mathrm{T}\left(z_2\right),$ |
| $z_2=k_2-\dfrac{1}{z_3}$ | $z_2=\mathrm{S}^{k_2}\mathrm{T}\left(z_3\right),$ |
| $\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots$ | |
| $z_{n-1}=-k_{n-1}-\dfrac{1}{z_n}$ | $z_{n-1}=\mathrm{S}^{-k_{n-1}}\mathrm{T}\left(z_n\right)$ |
よってこの場合には問題の定理は証明された.
一般の場合において\[\pm\mathrm{M}=\begin{pmatrix}a&b\\c&d\end{pmatrix},\hphantom{m^\prime}c\gt1\]$d=cm+d_0$,$0\lt d_0\lt c$($d$ は $c$ で割り切れない.$\left(c,\ d\right)=1$ だから)とすれば $b=am+b_0$ と置いて\begin{eqnarray*}\pm\mathrm{M}&=&\begin{pmatrix}a&b_0\\c&d_0\end{pmatrix}\begin{pmatrix}1&m\\0&1\end{pmatrix}\\[2mm]&=&\mathrm{S}^{k_0}\mathrm{TS}^{-k_1}\mathrm{T}\cdots\cdots\mathrm{S}^{-k_{n-1}}\mathrm{TS}^m.\end{eqnarray*}さて $c=\pm1$ ならば\begin{eqnarray*}\pm\mathrm{M}&=&\begin{pmatrix}a&b\\1&d\end{pmatrix}\hspace{2cm}ad-b=1\\&=&\begin{pmatrix}a&-1\\1&\hphantom{-}0\end{pmatrix}\mathrm{S}^d=\mathrm{S}^a\mathrm{TS}^d.\end{eqnarray*}また $c=0$ ならば\[\pm\mathrm{M}=\begin{pmatrix}1&b\\0&1\end{pmatrix}=\mathrm{S}^b.\] 〔注意〕 前出($186$ 頁)の $\mathrm{H}=\begin{pmatrix}-1&-1\\\hphantom{-}1&\hphantom{-}0\end{pmatrix}=\mathrm{S}^{-1}\mathrm{T}$,$\mathrm{H}^2=-\mathrm{TS}$.$\mathrm{H}^3=\mathrm{E}$ だから,$\mathrm{S}^{-1}\mathrm{TS}^{-1}\mathrm{TS}^{-1}\mathrm{T}=\mathrm{E}$,また $\mathrm{TSTSTS}=-\mathrm{E}$.故に $\mathrm{M}$ を $\mathrm{S}$,$\mathrm{T}$ から組み立てる方法は一意的でない.
$\mathrm{S}=\mathrm{TH}^2$,$\mathrm{H}^2=\mathrm{H}^{-1}$ を用いて\[\pm\mathrm{M}=\mathrm{H}^{a_0}\mathrm{TH}^{a_1}\mathrm{T}\cdots\mathrm{H}^{a_{m-1}}\mathrm{TH}^{a_m}.\]ただし,指数 $a$ は $\pm1$ で,$a_0$ と $a_m$ とは $0$ でもあり得る.このような表わし方は一意的である.