第 $4$ 章　二次体 $K\left(i\right)$，$K\left(\sqrt{-3}\right)$ の整数

　一般の二次体^$*$

$\ ^*\ $

二次体の定義は第 $5$ 章で述べる．

 の整数論を述べる前に，本章では最も簡単でかつ重要な特別の場合として二次体 $K\left(i\right)$　および　$K\left(\sqrt{-3}\right)$　を取り扱う．有理整数に関する二，三の有名な問題が，これらの二次体の問題として考察されるときに，最も透明に解決されることを示すのが目標である．

　$\S\ 36.$　複素整数 $\boldsymbol{a+bi}$

　$\boldsymbol{1.}$　Gauss は四乗剰余の相互法則を求めるに際して整数の概念を複素数の上に拡張することの必要を認めた．Gauss のこの創意は数学史上における重大な転回点というべきものである．それは一般的には，虚数の承認を決定的ならしめ，特殊的には，現代の代数的整数論の起源となったのである．
　Gauss が取り扱った複素整数は\[a+bi\tag{$\ 1\ $}\]において $a$，$b$ が有理整数なるものである．現時はこれを Gauss の複素整数という．
　本節において，このような複素整数の理論の概要を述べる．よって単に整数というのは，すなわち複素整数 $\left(\ 1\ \right)$ を意味することにして，従来の意味における整数は特に有理整数という．ただし，有理整数は $\left(\ 1\ \right)$ において $b=0$ である特別な場合にほかならない．
　本節では原則として複素整数をギリシャ文字で表わし，有理整数にきまっている数はローマ字で表わすことにする．誤解の生じそうにない場合にはいちいち断わらない．
　$\left(\ 1\ \right)$ のような数を「整数」というのは次の理由に基づくのである．
 （第一） 整数の和，差および積は整数である．\begin{alignat*}{1}&\left(a+bi\right)\pm\left(c+di\right)=\left(a\pm c\right)+\left(b\pm d\right)i,\\[2mm]&\left(a+bi\right)\left(c+di\right)=\left(ac-bd\right)+\left(ad+bc\right)i.\end{alignat*}　和，差および積の実数部も虚数部もともに有理整数であることが要点である．
 （第二） 整数の商は必ずしも整数ではない．\[\frac{a+bi}{c+di}=\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i.\]　商の実数部も虚数部も，有理数ではあるが，必ずしも有理整数ではないのである．

　これによって，割り切れるということ，したがって約数，倍数の概念を複素整数の上に拡張することができる．
　整数 $\alpha$，$\beta$ の商 $\alpha/\beta=\gamma$ が整数であるときに，$\alpha$ は $\beta$ で割り切れるといい，$\alpha$ を $\beta$ の倍数，$\beta$ を $\alpha$ の約数という．
　この定義によれば，$\alpha_1$，$\alpha_2$ が $\beta$ で割り切れるとき，$\alpha_1\pm\alpha_2$，または一般に $\mu_1\alpha_1+\mu_2\alpha_2$ は $\beta$ で割り切れる．
　$\boldsymbol{2.}$　整数 $\mu=a+bi$ の共軛複素数 $\overline{\mu}=a-bi$ は整数である．
$\mu\overline{\mu}=\left|\mu\right|^2=a^2+b^2$，すなわち $\mu$ のノルム（記号：$N\mu$）は有理整数である．よって $N\mu$ は $\mu$ の倍数である．また $\alpha$ が $\beta$ の倍数ならば，$N\alpha$ は $N\beta$ の倍数である（$\alpha=\beta\gamma$ とすれば，$N\alpha=N\beta\hspace{0.7mm}\cdotp N\gamma$）．

　$\boldsymbol{3.}$　すべての整数の約数なる整数を単数という．
　単数は $1$ の約数にほかならない．
　有理整数の範囲内では単数は $\pm1$ の二つに限るが，複素整数についていえばどうか．
　$\varepsilon=x+yi$ を単数とすれば，$N\varepsilon=x^2+y^2$ は $1$ の約数，したがって $x^2+y^2=1$．故に $x=\pm1$，$y=0$，または $x=0$，$y=\pm1$，すなわち $\varepsilon=\pm1$，または $\varepsilon=\pm i$ であることを要する．さて $\pm1$ はもちろん単数で，また $\left(\pm i\right)\left(\mp i\right)=1$ であるから，$\pm i$ も単数である．故に単数は $\pm1$，$\pm i$ の四つである．
　$\boldsymbol{4.}$　$\alpha/\beta$ が単数に等しいときに，$\alpha$，$\beta$ を互いに同伴数という．すなわち $\alpha=x+yi$ の同伴数は $\pm\alpha$，$\pm i\alpha$（すなわち $x+yi$，$-x-yi$，$-y+xi$，$y-xi$）である．
　二つの整数の間の割り切れる，割り切れないの関係は，それらの整数を同伴数をもって置き換えることによって影響されないから，整除の問題に関する限り，同伴数を同一の数のように取り扱ってよい（有理整数の場合に $\pm1$ なる因数を度外においてよいのと同様である）．

　$\boldsymbol{5.}$　整数 $\alpha$ を整因数 $\beta$，$\gamma$，$\cdots\cdots$ の積に分解して\[\alpha=\beta\hspace{0.7mm}\cdotp\gamma\cdots\cdots\]とすれば，\[N\alpha=N\beta\hspace{0.7mm}\cdotp N\gamma\cdots\cdots\]　故に各因数 $\beta$，$\gamma$，$\cdots\cdots$ が単数でないとすれば，$N\beta$，$N\gamma$，$\cdots\cdots$ は $1$ よりも大きい有理整数であるから，$\alpha$ が与えられたときには，因数の数は有限である．よって，単数（および $0$）を除いていえば，すべての整数は分解不可能な因数の積に等しい．
　$N\alpha$ が素数ならば，$\alpha$ は分解不可能である．
　例えば $1+i$，$N\left(1+i\right)=2$；$1+2i$，$N\left(1+2i\right)=5$ 等．
　しからば，分解不可能な整数を素数（複素整数中の素数）と名づけることはどうか．それは任意の整数を分解不可能な因数に分解する結果がただ一つであるならば適当であるが，そうでなければ不適当であろう．
　ただし，分解の結果がただ一つというのは，同伴数を同一の因数と見ていうのである．
　例えば，$5=\left(1+2i\right)\left(1-2i\right)=\left(2+i\right)\left(2-i\right)$ であるけれども，$2+i=i\left(1-2i\right)$，$2-i=-i\left(1+2i\right)$ であるから，これらを同一の分解と見る．
　実際，上記のような分解の結果はただ一つである．またこの事実が整数の拡張を有効ならしめる原因である．
　よって分解不可能な整数を素数と呼ぶことにするが，任意の整数を素因数に分解する結果が同伴数を無差別に取り扱う条件のもとに，ただ一つであることを確かめるのが，さしあたっての重大問題である．
　もしも読者が有理整数の場合に分解の一意性がどうして証明されたかを回顧するならば，除法の剰余に関する定理 $1.\ 2$ においてその源泉を見出すであろう．複素整数の場合においても，幸いにしてこの定理の拡張が次のような意味において可能である．
 〔定理 $\boldsymbol{4.\ 1}$〕 $\alpha$，$\beta$（$\beta\neq0$）を任意の整数とするとき，\[\alpha=\beta\kappa+\rho,\hphantom{m}\left|\rho\right|\lt\left|\beta\right|\]なる整数 $\kappa$，$\rho$ が必ず存在する．
 〔証〕 整数 $x+yi$ は複素数平面上において正方格子点で表わされる．任意の複素数 $\xi$ がこの格子の或る正方格子内にあるとき，その正方形の四つの頂点のうち少なくとも一つから $\xi$ までの距離は $1$ よりも小である．$\xi=\alpha/\beta$ のとき，この頂点を $\kappa$ とすれば，$\kappa$ は整数で\[\left|\frac{\alpha}{\beta}-\kappa\right|\lt1.\]　故に $\alpha-\beta\kappa=\rho$ と置けば，$\rho$ は整数で\[\left|\frac{\rho}{\beta}\right|\lt1，\ すなわち\ \ \left|\rho\right|\lt\left|\beta\right|.\]　この定理に基づいて二つの整数 $\alpha$，$\beta$ に Euclid の互除法を行なうことができる．すなわち\[\alpha=\kappa\beta+\beta_1,\hspace{1.2cm}\left|\beta_1\right|\lt\left|\beta\right|,\]$\left|\beta_1\right|\neq0$ ならば，\[\beta=\kappa_1\beta_1+\beta_2,\hspace{1cm}\left|\beta_2\right|\lt\left|\beta_1\right|,\]\[\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\]\[\left|\beta\right|\gt\left|\beta_1\right|\gt\left|\beta_2\right|\gt\cdots\cdots，したがって\ N\beta\gt N\beta_1\gt N\beta_2\gt\cdots\cdots\]で，これらは正の有理整数であるから，ついに剰余が $0$ にならねばならない．例えば $\beta_{n-1}=\kappa_n\beta_n$ とする．
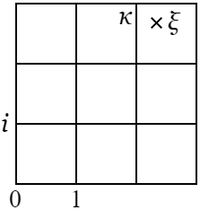　しからば，$\alpha$，$\beta$ は $\beta_n$ で割り切れる．すなわち $\beta_n$ は $\alpha$，$\beta$ の公約数である．のみならず，$\alpha$，$\beta$ の公約数は $\beta_1$，$\beta_2$，$\cdots\cdots$ の約数，したがって $\beta_n$ の約数である．故に $\beta_n$ はそれ自身 $\alpha$，$\beta$ の公約数で，かつ $\alpha$，$\beta$ の任意の公約数で割り切れるから，$\beta_n$ を $\alpha$，$\beta$ の最大公約数といい，それを $\left(\alpha,\ \beta\right)$ で表わす（もちろん $\beta_n$ は $\alpha$，$\beta$ の公約数の中で最大の絶対値を有するものである）．
　いま $\left(\alpha,\ \beta\right)=\delta$ とすれば，上記 Euclid の算法において，逐次現われてくる「部分商」$\kappa$，$\kappa_1$，$\cdots\cdots$ から\[\alpha\xi+\beta\eta=\delta\]なる整数 $\xi$，$\eta$ を組み立て得ること，有理整数の場合と同様である（$\S\ 2$，$\S\ 19$）．
　特に $\alpha$，$\beta$ が単数以外の公約数を有しない場合には，それらを互いに素であるという．その場合に $\alpha\gamma$ が $\beta$ で割り切れるならば，$\gamma$ が $\beta$ で割り切れること，定理 $1.\ 6$ と同様である．
　よってまた二つ以上の整数の積 $\alpha\beta\gamma\cdots\cdots$ が素数 $\pi$ で割り切れるときには，因数のうち少なくとも一つが $\pi$ で割り切れる．
　これを根拠として，複素整数の場合にも，素因数分解の一意性が証明される．いま\[\alpha=\pi\pi^\prime\pi^{\prime\prime}\cdots\cdots=\kappa\kappa^\prime\kappa^{\prime\prime}\cdots\cdots\tag{$\ 1\ $}\]で $\pi$，$\kappa$ 等を素数とすれば，$\kappa$，$\kappa^\prime$，$\kappa^{\prime\prime}\cdots\cdots$，の積が $\pi$ で割り切れることから，その中の一つ，例えば $\kappa$ が $\pi$ で割り切れる．よって $\kappa=\varepsilon\pi$ と置けば，$\kappa$ が素数であるから，$\varepsilon$ は単数である．故に\[\varepsilon\pi^\prime\pi^{\prime\prime}\cdots\cdots=\kappa^\prime\kappa^{\prime\prime}\cdots\cdots\]　同様に $\kappa^\prime$ は例えば $\pi^\prime$ の同伴数，$\kappa^\prime=\varepsilon^\prime\pi^\prime$，したがって\[\varepsilon\varepsilon^\prime\pi^{\prime\prime}\cdots\cdots=\kappa^{\prime\prime}\cdots\cdots\]を得て，最後に両側の素因数が同時に尽きて，一辺に掛けられている単数の積が $1$ になる．すなわち $\left(\ 1\ \right)$ において因数 $\pi$，$\pi^\prime$，$\pi^{\prime\prime}$，$\cdots\cdots$ は $\kappa$，$\kappa^\prime$，$\kappa^{\prime\prime}$，$\cdots\cdots$ と単数因子によってのみ異なり得るのである．
　素因数分解の一意性が確定した上は，それに基づいて有理整数に関して得られた定理が Gauss の整数にも当てはまるのである．
 〔問題 $\boldsymbol{1}$〕 $\alpha$，$\beta$，$\gamma$，$\mu$ が与えられた整数であるとき，方程式\[\alpha\xi+\beta\eta+\gamma\zeta=\mu\]が整数解を有するため必要かつ十分な条件は，$\mu$ が $\left(\alpha,\ \beta,\ \gamma\right)$ で割り切れることである．
 〔解〕 定理 $1.\ 7$ と同様，$\alpha\xi+\beta\eta+\gamma\zeta$ の形に表わされる整数の中で，$0$ を除いて最小絶対値（したがって最小ノルム）を有するものを $\kappa=\alpha\xi_0+\beta\eta_0+\gamma\zeta_0$ とする．しからば，その他は $\kappa$ の倍数である．故に $\kappa$ は $\alpha$，$\beta$，$\gamma$ の公約数であるが，$\kappa$ は $\alpha$，$\beta$，$\gamma$ の公約数で割り切れるから，$\kappa=\left(\alpha,\ \beta,\ \gamma\right)$．故に $\mu$ が $\kappa$ で割り切れることが解のあるための条件である．定理 $1.\ 7$ の証明を参照して，各論点に当って見るとよい．
 〔問題 $\boldsymbol{2}$〕 複素数平面上において，$\mu$ で割り切れる整数は $0$ と $\mu$ とを結ぶ線分を一辺とする正方格子の点で表わされる．
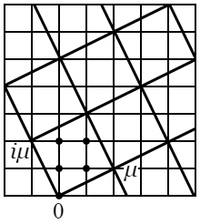 〔解〕 $\mu\left(x+yi\right)=x\mu+y\left(i\mu\right)$ は $\mu$ の有理整数倍と $i\mu$ の有理整数倍との和であるから．
 〔注意〕 これらの正方形に関して相似の位置にある点によって表わされる二つの整数 $\alpha$，$\beta$ の差は $\mu$ で割り切れる．すなわち\[\alpha\equiv \beta\hphantom{m}\left(\text{mod}.\ \mu\right).\]よって $\text{mod}.\ \mu$ に関して複素整数を類に分けるならば，各類は粗なる格子の一つの正方形に属する格子点によって代表される．この正方形の面積は $N\left(\mu\right)$ に等しいから，類の数は $N\left(\mu\right)$ である（$\S\ 24$，問題 $1$）．