初期位置・初速が等しい投射の最高到達点

〈 Berger | Dillon 〉さんのツイート: "Throwing an object at the same speed but different angles defines an ellipse via its maximum height… "に触発されて計算したものです。
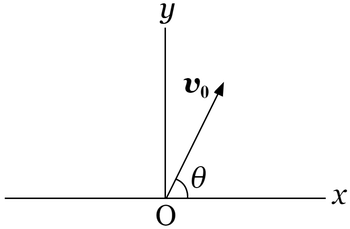
投射の向きだけを変えて、最高到達点の集合となる図形を考えます。

$D=2$

$2$次元の場合、$x$、$y$の$2$個の座標を使います。
初速$v_0=\left|\boldsymbol{v_0}\right|=\sqrt{{v_{0x}}^2+{v_{0y}}^2}$が同じで、
鉛直方向上向きに$y$軸の正の向きを取り、
原点からの傾き$\theta$（$0\leqq\theta\leqq\pi$）で投射する（投げる手を離す）。
最高到達点の高さ$y_M$を計算する。
運動方程式$m\dot{v_y}=-mg$を解くと、\begin{eqnarray*}v_y&=&-gt+C\hspace{1cm}C：積分定数\\v_0\sin\theta&=&-g\cdotp0+C\hspace{1cm}\left(t=0\right)\\C&=&v_0\sin\theta\\v_y&=&-gt+v_0\sin\theta\end{eqnarray*}最高到達点では$v_y=0$であり、投射から最高到達点に達するまでの時間を$t_M$とすると\begin{eqnarray*}0&=&-gt_M+v_0\sin\theta\\t_M&=&\frac{v_0\sin\theta}{g}\end{eqnarray*}最高到達点の高さを求めるために$y$座標を計算する。\begin{eqnarray*}y&=&-\frac{gt^2}{2}+v_0\sin\theta t+C^\prime\hspace{1cm}C^\prime：積分定数\\0&=&-\frac{g\cdotp0^2}{2}+v_0\sin\theta\cdotp0+C^\prime\hspace{1cm}\left(t=0\right)\\C^\prime&=&0\\y&=&-\frac{gt^2}{2}+v_0\sin\theta t\\y_M&=&-\frac{g{t_M}^2}{2}+v_0\sin\theta t_M\\&=&-\frac{g}{2}\left(\frac{v_0\sin\theta}{g}\right)^2+v_0\sin\theta\frac{v_0\sin\theta}{g}\\&=&-\frac{1}{2}\frac{{v_0}^2\sin^2\theta}{g}+\frac{{v_0}^2\sin^2\theta}{g}\\&=&\frac{{v_0}^2\sin^2\theta}{2g}\\&=&\frac{{v_0}^2}{2g}\sin^2\theta\end{eqnarray*}ここで、\begin{eqnarray*}\sin^2\theta&=&\frac{1}{2}\sin^2\theta+\frac{1}{2}\cos^2\theta\\&&+\frac{1}{2}\sin^2\theta-\frac{1}{2}\cos^2\theta\\&=&\frac{1}{2}-\frac{\cos2\theta}{2}\end{eqnarray*}より、\[y_M=\frac{{v_0}^2}{2g}\left(\frac{1}{2}-\frac{\cos2\theta}{2}\right)\]$x$方向には等速度運動をする。最高到達点での$x$座標を$x_M$とする。\[x_M=v_0\cos\theta\frac{v_0\sin\theta}{g}=\frac{{v_0}^2}{2g}\sin2\theta\]最高到達点の座標をまとめて書くと\[\boldsymbol{x}=\frac{{v_0}^2}{2g}\left(\sin2\theta,\ \frac{1}{2}-\frac{\cos2\theta}{2}\right)\]原点の$y$座標を$\dfrac{{v_0}^2}{2g}\cdotp\dfrac{1}{2}$上げると\[\boldsymbol{x^\prime}=\frac{{v_0}^2}{2g}\left(\sin2\theta,\ -\frac{\cos2\theta}{2}\right)\]$a=\dfrac{{v_0}^2}{2g}$、$b=\dfrac{{v_0}^2}{2g}\cdotp\dfrac{1}{2}$とすると、$\dfrac{{x_M}^2}{a^2}+\dfrac{{y_M}^2}{b^2}=1$であり、楕円である。
扁平率$f$は\[f=1-\frac{\dfrac{{v_0}^2}{2g}\cdotp\dfrac{1}{2}}{\dfrac{{v_0}^2}{2g}}=\frac{1}{2}\]※）楕円の最下部の点だけ含まれていないように思えるかも知れませんが、$\theta=0$、$\pi$の投射で$t=0$の時に初期位置で最高到達点となっていて、楕円の最下部の点も含みます。

$D=3$

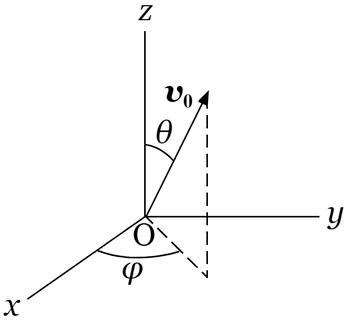
$3$次元の場合、$x$、$y$、$z$の$3$個の座標を使います。
初速$v_0=\left|\boldsymbol{v_0}\right|=\sqrt{{v_{0x}}^2+{v_{0y}}^2+{v_{0z}}^2}$が同じで、
鉛直方向上向きに$z$軸の正の向きを取り、
$z$軸に垂直に$x-y$平面をとる右手系とする。
$z$軸の正の向きからの角度$\theta\ \Bigl(0\leqq\theta\lt\dfrac{\pi}{2}\Bigr)$、
$x$軸の正の向きから$y$軸正の向きへ向かう角度$\varphi$（$0\leqq\varphi\lt2\pi$）で投射する（投げる手を離す）。
最高到達点の高さ$z_M$を計算する。
運動方程式$m\dot{v_z}=-mg$を解くと、\begin{eqnarray*}v_z&=&-gt+C\hspace{1cm}C：積分定数\\v_0\cos\theta&=&-g\cdotp0+C\hspace{1cm}\left(t=0\right)\\C&=&v_0\cos\theta\\v_z&=&-gt+v_0\cos\theta\end{eqnarray*}最高到達点では$v_z=0$であり、投射から最高到達点に達するまでの時間を$t_M$とすると\begin{eqnarray*}0&=&-gt_M+v_0\cos\theta\\t_M&=&\frac{v_0\cos\theta}{g}\end{eqnarray*}最高到達点の高さを求めるために$z$座標を計算する。\begin{eqnarray*}z&=&-\frac{gt^2}{2}+v_0\cos\theta t+C^\prime\hspace{1cm}C^\prime：積分定数\\0&=&-\frac{g\cdotp0^2}{2}+v_0\cos\theta\cdotp0+C^\prime\hspace{1cm}\left(t=0\right)\\C^\prime&=&0\\z&=&-\frac{gt^2}{2}+v_0\cos\theta t\\z_M&=&-\frac{g{t_M}^2}{2}+v_0\cos\theta t_M\\&=&-\frac{g}{2}\left(\frac{v_0\cos\theta}{g}\right)^2+v_0\cos\theta\frac{v_0\cos\theta}{g}\\&=&-\frac{1}{2}\frac{{v_0}^2\cos^2\theta}{g}+\frac{{v_0}^2\cos^2\theta}{g}\\&=&\frac{{v_0}^2\cos^2\theta}{2g}\\&=&\frac{{v_0}^2}{2g}\cos^2\theta\end{eqnarray*}ここで、\begin{eqnarray*}\cos^2\theta&=&\frac{1}{2}\cos^2\theta+\frac{1}{2}\sin^2\theta\\&&+\frac{1}{2}\cos^2\theta-\frac{1}{2}\sin^2\theta\\&=&\frac{1}{2}+\frac{\cos2\theta}{2}\end{eqnarray*}より、\[z_M=\frac{{v_0}^2}{2g}\left(\frac{1}{2}+\frac{\cos2\theta}{2}\right)\]$x$、$y$方向には等速度運動をする。最高到達点での$x$、$y$座標を$x_M$、$y_M$とする。\begin{alignat*}{2}x_M&=v_0\sin\theta\cos\varphi\frac{v_0\cos\theta}{g}&&=\frac{{v_0}^2}{2g}\sin2\theta\cos\varphi\\y_M&=v_0\sin\theta\sin\varphi\frac{v_0\cos\theta}{g}&&=\frac{{v_0}^2}{2g}\sin2\theta\sin\varphi\end{alignat*}最高到達点の座標をまとめて書くと\[\boldsymbol{x}=\frac{{v_0}^2}{2g}\left(\sin2\theta\cos\varphi,\ \sin2\theta\sin\varphi,\ \frac{1}{2}+\frac{\cos2\theta}{2}\right)\]原点の$z$座標を$\dfrac{{v_0}^2}{2g}\cdotp\dfrac{1}{2}$上げると\[\boldsymbol{x^\prime}=\frac{{v_0}^2}{2g}\left(\sin2\theta\cos\varphi,\ \sin2\theta\sin\varphi,\ \frac{\cos2\theta}{2}\right)\]$a=\dfrac{{v_0}^2}{2g}$、$b=\dfrac{{v_0}^2}{2g}$、$c=\dfrac{{v_0}^2}{2g}\cdotp\dfrac{1}{2}$とすると、$\dfrac{{x_M}^2}{a^2}+\dfrac{{y_M}^2}{b^2}+\dfrac{{z_M}^2}{c^2}=1$であり、楕円体である。
この楕円体の$z$軸に平行な平面による断面をとる。
楕円体は$x-y$平面に関して（$z$軸まわりに）対称であり、$y$軸に平行な平面をとり、
その平面の$y$座標を$y_p$とすると、\begin{eqnarray*}&&\dfrac{x^2}{a^2}+\dfrac{{y_p}^2}{b^2}+\dfrac{z^2}{c^2}=1\\&&\dfrac{x^2}{a^2}+\dfrac{z^2}{c^2}=1-\dfrac{{y_p}^2}{b^2}\\&&\dfrac{x^2}{A^2}+\dfrac{z^2}{B^2}=1\\&&A=\frac{a}{\sqrt{1-\dfrac{{y_p}^2}{b^2}}},\ \ B=\frac{c}{\sqrt{1-\dfrac{{y_p}^2}{b^2}}}=\frac{A}{2}\end{eqnarray*}扁平率$f$は\[f=1-\frac{B}{A}=1-\frac{\ \dfrac{A}{2}\ }{A}=\frac{1}{2}\]となる（楕円体の対称な方向に垂直な断面の扁平率、楕円体の扁平率）。

分厚いどら焼きか、丸いカレーパンのような形です。